
ΓΨΧβΡΩΓΩΈΣΝΥ”≠Ϋ”¬Ο”ΈΆζΦΨΒΡΒΫά¥Θ§…ΌΝ÷Υ¬…η÷ΟΝΥ“ΜΗωΉ®Ο≈Α≤≈≈¬ΟΩΆΉΓΥόΒΡΩΆ’ΜΘ§Υ¬ΟμΒΡΙΛΉς»Υ‘±ΖΔœ÷ΈΣ”ΈΩΆΉΦ±ΗΒΡ ≥Έο”––©‘¬Ζί Θ”ύ≤Μ…ΌΘ§άΥΖ―Κή―œ÷ΊΘ§ΈΣΝΥΩΊ÷ΤΨ≠”Σ≥…±ΨΘ§Φθ…ΌάΥΖ―Θ§ΨΆœκ ±Βς’ϊΆΕ»κ.ΈΣ¥ΥΥϊΟ«Ά≥ΦΤΟΩΗω‘¬»κΉΓΒΡ”ΈΩΆ»Υ ΐΘ§ΖΔœ÷ΟΩΡξΗςΗω‘¬Ζίά¥ΩΆ’Μ»κΉΓΒΡ”ΈΩΆ»Υ ΐΜα≥ œ÷÷ήΤΎ–‘ΒΡ±δΜ·Θ§≤Δ«“”–“‘œ¬Ιφ¬…ΘΚ
ΔΌΟΩΡξœύΆ§ΒΡ‘¬ΖίΘ§»κΉΓΩΆ’ΜΒΡ”ΈΩΆ»Υ ΐΜυ±ΨœύΆ§ΘΜ
ΔΎ»κΉΓΩΆ’ΜΒΡ”ΈΩΆ»Υ ΐ‘Ύ![]() ‘¬ΖίΉν…ΌΘ§‘Ύ
‘¬ΖίΉν…ΌΘ§‘Ύ![]() ‘¬ΖίΉνΕύΘ§œύ≤ν‘Φ
‘¬ΖίΉνΕύΘ§œύ≤ν‘Φ![]() »ΥΘΜ
»ΥΘΜ
Δέ![]() ‘¬Ζί»κΉΓΩΆ’ΜΒΡ”ΈΩΆ‘ΦΈΣ
‘¬Ζί»κΉΓΩΆ’ΜΒΡ”ΈΩΆ‘ΦΈΣ![]() »ΥΘ§ΥφΚσ÷𑬑ωΦ”÷±ΒΫ
»ΥΘ§ΥφΚσ÷𑬑ωΦ”÷±ΒΫ![]() ‘¬Ζί¥οΒΫΉνΕύ.
‘¬Ζί¥οΒΫΉνΕύ.
Θ®1Θ© ‘”Ο“ΜΗω’ΐœ“–Ά»ΐΫ«Κ· ΐΟη ω“ΜΡξ÷–»κΉΓΩΆ’ΜΒΡ”ΈΩΆ»Υ ΐ”ꑬΖί÷°ΦδΒΡΙΊœΒΘΜ
Θ®2Θ©«κΈ ΡΡΦΗΗω‘¬Ζί“ΣΉΦ±Η![]() Ζί“‘…œΒΡ ≥ΈοΘΩ
Ζί“‘…œΒΡ ≥ΈοΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ‘¬ΓΔ
‘¬ΓΔ![]() ‘¬ΓΔ
‘¬ΓΔ![]() ‘¬ΓΔ
‘¬ΓΔ![]() ‘¬ΓΔ
‘¬ΓΔ![]() ‘¬
‘¬![]() Ηω‘¬Ζί.
Ηω‘¬Ζί.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΔΌΘ§Ω…÷ΣΚ· ΐ![]() ΒΡΉν–Γ’ΐ÷ήΤΎ «
ΒΡΉν–Γ’ΐ÷ήΤΎ «![]() ΘΜΗυΨίΔΎΩ…÷ΣΘ§
ΘΜΗυΨίΔΎΩ…÷ΣΘ§![]() Ήν–ΓΘ§
Ήν–ΓΘ§![]() Ήν¥σΘ§«“
Ήν¥σΘ§«“![]() ΘΜΗυΨίΔέΩ…÷ΣΘ§Κ· ΐ
ΘΜΗυΨίΔέΩ…÷ΣΘ§Κ· ΐ![]() ‘Ύ
‘Ύ![]() …œΒΞΒςΒί‘ωΘ§«“
…œΒΞΒςΒί‘ωΘ§«“![]() Θ§”…¥ΥΩ…ΒΟΚ· ΐ
Θ§”…¥ΥΩ…ΒΟΚ· ΐ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®2Θ©”…ΧθΦΰ÷Σ![]() Θ§ΫαΚœ
Θ§ΫαΚœ![]() Θ§
Θ§![]() Θ§Φ¥Ω…ΒΟΒΫΫα¬έΘ°
Θ§Φ¥Ω…ΒΟΒΫΫα¬έΘ°
Θ®1Θ©…ηΗΟΚ· ΐΈΣ![]() Θ§
Θ§
ΗυΨίΧθΦΰΔΌΘ§Ω…÷Σ’βΗωΚ· ΐΒΡ÷ήΤΎ «![]() ΘΜ
ΘΜ
”…ΔΎΩ…÷ΣΘ§![]() Ήν–ΓΘ§
Ήν–ΓΘ§![]() Ήν¥σΘ§«“
Ήν¥σΘ§«“![]() ΘΜ
ΘΜ
”…ΔέΩ…÷ΣΘ§Κ· ΐ![]() ‘Ύ
‘Ύ![]() …œΒΞΒςΒί‘ωΘ§«“
…œΒΞΒςΒί‘ωΘ§«“![]() Θ§Υυ“‘
Θ§Υυ“‘![]() .
.
ΗυΨί…œ ωΖ÷ΈωΩ…ΒΟΘ§![]() Θ§Ι
Θ§Ι ![]() Θ§«“
Θ§«“![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() .
.
ΗυΨίΖ÷ΈωΩ…÷ΣΘ§Β±![]() ±Θ§
±Θ§![]() »ΓΉν–Γ÷ΒΘ§Β±
»ΓΉν–Γ÷ΒΘ§Β±![]() ±Θ§
±Θ§![]() »ΓΉν¥σ÷Β.
»ΓΉν¥σ÷Β.
Ι ![]() Θ§«“
Θ§«“![]() Θ§”÷“ρΈΣ
Θ§”÷“ρΈΣ![]() Θ§Ι
Θ§Ι ![]() .
.
Υυ“‘»κΉΓΩΆ’ΜΒΡ”ΈΩΆ»Υ ΐ”ꑬΖί÷°ΦδΒΡΙΊœΒ ΫΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©Νν![]() Θ§Μ·ΦρΒΟ
Θ§Μ·ΦρΒΟ![]() Θ§
Θ§
Φ¥![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() .
.
“ρΈΣ![]() Θ§«“
Θ§«“![]() Θ§Υυ“‘
Θ§Υυ“‘![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Θ§
Θ§
Φ¥‘Ύ![]() ‘¬ΓΔ
‘¬ΓΔ![]() ‘¬ΓΔ
‘¬ΓΔ![]() ‘¬ΓΔ
‘¬ΓΔ![]() ‘¬ΓΔ
‘¬ΓΔ![]() ‘¬
‘¬![]() Ηω‘¬Ζί“ΣΉΦ±Η
Ηω‘¬Ζί“ΣΉΦ±Η![]() Ζί“‘…œΒΡ ≥Έο.
Ζί“‘…œΒΡ ≥Έο.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©»γΙϊΑ―άβ÷υ÷–Ιΐ≤ΜœύΝΎΒΡΝΫΧθ≤ύάβΒΡΫΊΟφΫ–άβ÷υΒΡΓΑΕ‘Ϋ«ΟφΓ±Θ§‘ρΤΫ––ΝυΟφΧεΒΡΕ‘Ϋ«ΟφΒΡ–ΈΉ¥ «_______Θ§÷±ΤΫ––ΝυΟφΧεΒΡΕ‘Ϋ«ΟφΒΡ–ΈΉ¥ «______ΘΜ
Θ®2Θ©Ιΐ’ΐ»ΐάβ÷υΒΉΟφΒΡ“Μ±ΏΚΆΝΫΒΉΟφ÷––ΡΝ§œΏΕΈΒΡ÷–ΒψΉςΫΊΟφΘ§‘ρ’βΗωΫΊΟφΒΡ–ΈΉ¥ΈΣ_____.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬ΆΦ «Έ“Ιζ2008Ρξ÷Ν2014Ρξ…ζΜνά§ΜχΈόΚΠΜ·¥ΠάμΝΩΘ®ΒΞΈΜΘΚ“ΎΕ÷Θ©ΒΡ’έœΏΆΦ.

Θ®ΔώΘ©”…’έœΏΆΦΩ¥≥ωΘ§Ω…”ΟœΏ–‘ΜΊΙιΡΘ–ΆΡβΚœy”κtΒΡΙΊœΒΘ§«κ”ΟœύΙΊœΒ ΐΦ”“‘ΥΒΟςΘΜ
Θ®ΔρΘ©Ϋ®ΝΔyΙΊ”ΎtΒΡΜΊΙιΖΫ≥ΧΘ®œΒ ΐΨΪ»ΖΒΫ0.01Θ©Θ§‘Λ≤β2016ΡξΈ“Ιζ…ζΜνά§ΜχΈόΚΠΜ·¥ΠάμΝΩ.
ΗΫΉΔΘΚ
≤ΈΩΦ ΐΨίΘΚ![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Γ÷2.646.
Γ÷2.646.
≤ΈΩΦΙΪ ΫΘΚœύΙΊœΒ ΐ
ΜΊΙιΖΫ≥Χ![]() ÷––±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΙΪ ΫΖ÷±πΈΣΘΚ
÷––±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΙΪ ΫΖ÷±πΈΣΘΚ
![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ
»γΆΦ4Θ§‘ΎΥΡάβΉΕ![]() ÷–Θ§ΒΉΟφ
÷–Θ§ΒΉΟφ![]() «ΨΊ–ΈΘ§
«ΨΊ–ΈΘ§
![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§![]() Θ§
Θ§![]() ,
,![]() ”ΎΒψ
”ΎΒψ![]() Θ°
Θ°
(1) «σ÷ΛΘΚ![]()
![]() ΘΜ
ΘΜ
(2) «σ÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…ΒΡΫ«ΒΡ”ύœ“÷Β.
Υυ≥…ΒΡΫ«ΒΡ”ύœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
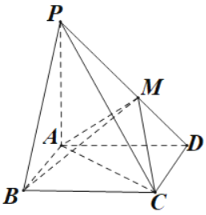
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ»ΐάβΧ®ABC©¹A1B1C1÷–Θ§DΘ§EΖ÷±π «ABΘ§ACΒΡ÷–ΒψΘ§B1EΓΆΤΫΟφABCΘ§ΓςAB1C «Β»±Ώ»ΐΫ«–ΈΘ§AB=2A1B1Θ§AC=2BCΘ§ΓœACB=90ΓψΘ°
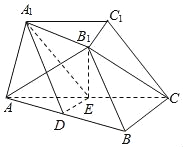
Θ®1Θ©÷ΛΟςΘΚB1CΓΈΤΫΟφA1DEΘΜ
Θ®2Θ©«σΕΰΟφΫ«A©¹BB1©¹CΒΡ’ΐœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η![]() ΓΔ
ΓΔ![]() ΈΣΥΪ«ζœΏ
ΈΣΥΪ«ζœΏ![]() …œΒΡΝΫΒψΘ§
…œΒΡΝΫΒψΘ§![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() ΒΡ÷–ΒψΘ§œΏΕΈ
ΒΡ÷–ΒψΘ§œΏΕΈ![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏ”κΥΪ«ζœΏΫΜ”Ύ
ΒΡ¥Ι÷±ΤΫΖ÷œΏ”κΥΪ«ζœΏΫΜ”Ύ![]() ΓΔ
ΓΔ![]() ΝΫΒψ
ΝΫΒψ
Θ®1Θ©»ΖΕ®![]() ΒΡ»Γ÷ΒΖΕΈß
ΒΡ»Γ÷ΒΖΕΈß
Θ®2Θ© ‘≈–Εœ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΥΡΒψ «ΖώΙ≤‘≤ΘΩ≤ΔΥΒΟςάμ”…
ΥΡΒψ «ΖώΙ≤‘≤ΘΩ≤ΔΥΒΟςάμ”…
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©Φ» «Εΰ¥ΈΚ· ΐ”÷ «ΟίΚ· ΐΘ§Κ· ΐgΘ®xΘ© «R…œΒΡΤφΚ· ΐΘ§Κ· ΐ![]() =
=![]() +1Θ§‘ρhΘ®2018Θ©+hΘ®2017Θ©+hΘ®2016Θ©+Γ≠+hΘ®1Θ©+hΘ®0Θ©+hΘ®©¹1Θ©+Γ≠hΘ®©¹2016Θ©+hΘ®©¹2017Θ©+hΘ®©¹2018Θ©=___________
+1Θ§‘ρhΘ®2018Θ©+hΘ®2017Θ©+hΘ®2016Θ©+Γ≠+hΘ®1Θ©+hΘ®0Θ©+hΘ®©¹1Θ©+Γ≠hΘ®©¹2016Θ©+hΘ®©¹2017Θ©+hΘ®©¹2018Θ©=___________
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΝΥΫβ―ß…ζΒΡ―ßœΑ«ιΩωΘ§“Μ¥Έ≤β ‘÷–Θ§ΩΤ»Έάœ Π¥”±ΨΑύ÷–≥ι»ΓΝΥnΗω―ß…ζΒΡ≥…Φ®Θ®¬ζΖ÷100Ζ÷Θ§«“≥ι»ΓΒΡ―ß…ζ≥…Φ®Ψυ‘Ύ![]() ΡΎΘ©Ϋχ––Ά≥ΦΤΖ÷Έω.Α¥’’
ΡΎΘ©Ϋχ––Ά≥ΦΤΖ÷Έω.Α¥’’![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΒΡΖ÷ΉιΉς≥ωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΚΆΤΒ ΐΖ÷≤Φ±μ.
ΒΡΖ÷ΉιΉς≥ωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΚΆΤΒ ΐΖ÷≤Φ±μ.

ΤΒ ΐΖ÷≤Φ±μ | |
| x |
| 4 |
| 10 |
| 12 |
| 8 |
| 4 |
Θ®1Θ©«σnΘ§aΘ§xΒΡ÷ΒΘΜ
Θ®2Θ©‘Ύ―Γ»ΓΒΡ―υ±Ψ÷–Θ§¥”ΒΆ”Ύ60Ζ÷ΒΡ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΫΟϊ―ß…ζΘ§ ‘Έ ’βΝΫΟϊ―ß…ζ‘ΎΆ§“ΜΉιΒΡΗ≈¬ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ‘ΎΥΡάβΉΕ![]() ÷–Θ§ΒΉΟφ
÷–Θ§ΒΉΟφ![]() «±Ώ≥ΛΈΣ4ΒΡ’ΐΖΫ–ΈΘ§
«±Ώ≥ΛΈΣ4ΒΡ’ΐΖΫ–ΈΘ§![]() «’ΐ»ΐΫ«–ΈΘ§ΤΫΟφ
«’ΐ»ΐΫ«–ΈΘ§ΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§![]() Ζ÷±π «
Ζ÷±π «![]() ΒΡ÷–Βψ.
ΒΡ÷–Βψ.
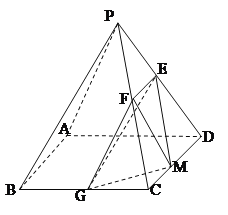
Θ®1Θ©«σ÷ΛΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ![]() «œΏΕΈ
«œΏΕΈ![]() …œ“ΜΒψΘ§«σ»ΐάβΉΕ
…œ“ΜΒψΘ§«σ»ΐάβΉΕ![]() ΒΡΧεΜΐ.
ΒΡΧεΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com