
随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康,得到 列联表如下:
列联表如下:
| | 室外工作 | 室内工作 | 合计 |
| 有呼吸系统疾病 | 150 | | |
| 无呼吸系统疾病 | | 100 | |
| 合计 | 200 | | |
 列联表;
列联表;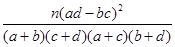
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1)列联表如下
(2)有95%的把握认为感染呼吸系统疾病与工作场所有关. 室外工作 室内工作 合计 有呼吸系统疾病 150 200 350 无呼吸系统疾病 50 100 150 合计 200 300 500
(3)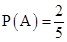 .
.
解析试题分析:(I)列联表如下
(2)通过计算 室外工作 室内工作 合计 有呼吸系统疾病 150 200 350 无呼吸系统疾病 50 100 150 合计 200 300 500  可知,有95%的把握认为感染呼吸系统疾病与工作场所有关.
可知,有95%的把握认为感染呼吸系统疾病与工作场所有关.
(3)采用分层抽样从室内工作的居民中抽取6名进行座谈,有呼吸系统疾病的抽4人,记为A、B、C、D,无呼吸系统疾病的抽2人,记为E、F,从中抽两人,共有15种抽法,A=“从中随机的抽取两人,两人都有呼吸系统疾病”有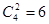 种,因此
种,因此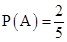 .
.
试题解析:(1)列联表如下
4分 室外工作 室内工作 合计 有呼吸系统疾病 150 200 350 无呼吸系统疾病 50 100 150 合计 200 300 500
(2)计算得,


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(2013•重庆)从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得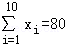 ,
, ,
, ,
,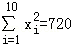 .
.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中, ,
,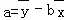 ,其中
,其中 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如下,据此解答如下问题:


(1)计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在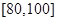 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在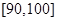 之间的概率;
之间的概率;
(3)根据频率分布直方图估计这次测试的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
关于某设备的使用年限 和所支出的维修费用
和所支出的维修费用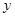 (万元),有如下的统计资料:
(万元),有如下的统计资料:
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
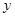 对
对 呈线形相关关系.试求:线形回归方程;(
呈线形相关关系.试求:线形回归方程;( ,
, )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| | 甲厂 | 乙厂 | 合计 |
| 优质品 | | | |
| 非优质品 | | | |
| 合 计 | | | |
| P(χ2≥x0) | 0.05 | 0.01 |
| x0 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如下所示:
| | 又发作过心脏病 | 未发作过心脏病 | 合计 |
| 心脏搭桥手术 | 39 | 157 | 196 |
| 血管清障手术 | 29 | 167 | 196 |
| 合计 | 68 | 324 | 392 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
大家知道,莫言是中国首位获得诺贝尔奖的文学家,国人欢欣鼓舞.某高校文学社从男女生中各抽取50名同学调查对莫言作品的了解程度,结果如下:
| 阅读过莫言的 作品数(篇) | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
| 男生 | 3 | 6 | 11 | 18 | 12 |
| 女生 | 4 | 8 | 13 | 15 | 10 |
| | 非常了解 | 一般了解 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |
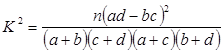
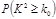 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
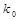 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某批次的某种灯泡共 个,对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个,对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于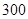 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
| 寿命(天) | 频数 | 频率 |
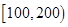 |  |  |
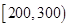 |  |  |
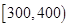 |  |  |
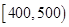 | 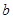 | 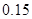 |
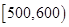 |  | 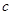 |
| 合计 |  |  |
 、
、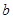 、
、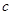 的值;
的值; 个灯泡中随机地购买了
个灯泡中随机地购买了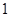 个,求此灯泡恰好不是次品的概率;
个,求此灯泡恰好不是次品的概率; 个,如果这
个,如果这 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求 的最小值.
的最小值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如图.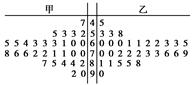
(1)若甲校高三年级每位学生被抽取的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格);
(2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为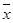 1,
1,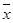 2,估计
2,估计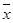 1-
1-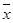 2的值.
2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com