
【题目】已知集合A={1,2,3,4}和集合B={1,2,3,…,n},其中n≥5,![]() .从集合A中任取三个不同的元素,其中最小的元素用S表示;从集合B中任取三个不同的元素,其中最大的元素用T表示.记X=T-S.
.从集合A中任取三个不同的元素,其中最小的元素用S表示;从集合B中任取三个不同的元素,其中最大的元素用T表示.记X=T-S.
(1)当n=5时,求随机变量X的概率分布和数学期望![]() ;
;
(2)求![]() .
.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率等于
的焦点,离心率等于![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于点
交于点![]() (不同于原点),与直线
(不同于原点),与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与极轴所在直线交于点
与极轴所在直线交于点![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三梭柱ABC-A1B1C1中,AC=BC,E,F分别为AB,A1B1的中点.
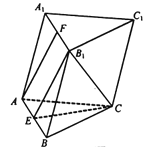
(1)求证:AF∥平面B1CE;
(2)若A1B1⊥![]() ,求证:平面B1CE⊥平面ABC.
,求证:平面B1CE⊥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环保部门要对所有的新车模型进行广泛测试,以确定它的行车里程的等级,右表是对 100 辆新车模型在一个耗油单位内行车里程(单位:公里)的测试结果.

(Ⅰ)做出上述测试结果的频率分布直方图,并指出其中位数落在哪一组;
(Ⅱ)用分层抽样的方法从行车里程在区间[38,40)与[40,42)的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在[40,42)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式m-|x-2|≥1,其解集为[0,4].
(1)求m的值;
(2)若a,b均为正实数,且满足a+b=m,求a2+b2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念和提高生态环境的保护意识,高二年级准备成立一个环境保护兴趣小组.该年级理科班有男生400人,女生200人;文科班有男生100人,女生300人.现按男、女用分层抽样从理科生中抽取6人,按男、女分层抽样从文科生中抽取4人,组成环境保护兴趣小组,再从这10人的兴趣小组中抽出4人参加学校的环保知识竞赛.
(1)设事件![]() 为“选出的这4个人中要求有两个男生两个女生,而且这两个男生必须文、理科生都有”,求事件
为“选出的这4个人中要求有两个男生两个女生,而且这两个男生必须文、理科生都有”,求事件![]() 发生的概率;
发生的概率;
(2)用![]() 表示抽取的4人中文科女生的人数,求
表示抽取的4人中文科女生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com