
已知正项数列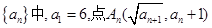 在抛物线
在抛物线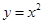 上;数列
上;数列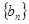 中,点
中,点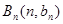 在过点(0,1),以
在过点(0,1),以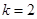 为斜率的直线上。
为斜率的直线上。
(1)求数列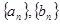 的通项公式;
的通项公式;
(2)若 成立,若存在,求出k值;若不存在,请说明理由;
成立,若存在,求出k值;若不存在,请说明理由;
(3)对任意正整数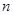 ,不等式
,不等式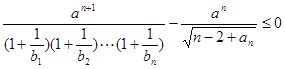 恒成立,求正数
恒成立,求正数 的取值范围。
的取值范围。
科目:高中数学 来源: 题型:解答题
已知数列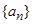 中,
中,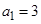 ,前
,前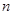 和
和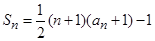
(Ⅰ)求证:数列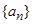 是等差数列; (Ⅱ)求数列
是等差数列; (Ⅱ)求数列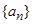 的通项公式;
的通项公式;
(Ⅲ)设数列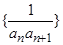 的前
的前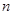 项和为
项和为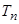 ,是否存在实数
,是否存在实数 ,使得
,使得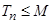 对一切正整数
对一切正整数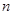 都成立?若存在,求
都成立?若存在,求 的最小值,若不存在,试说明理由.
的最小值,若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
给定常数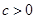 ,定义函数
,定义函数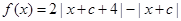 ,数列
,数列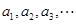 满足
满足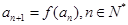 .
.
(1)若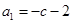 ,求
,求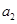 及
及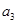 ;
;
(2)求证:对任意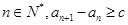 ,;
,;
(3)是否存在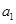 ,使得
,使得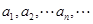 成等差数列?若存在,求出所有这样的
成等差数列?若存在,求出所有这样的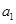 ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知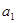 =2,点(
=2,点(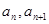 )在函数
)在函数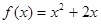 的图像上,其中
的图像上,其中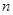 =
=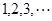 .
.
( 1 ) 证明:数列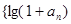 }是等比数列;
}是等比数列;
(2)设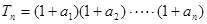 ,求
,求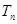 及数列{
及数列{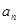 }的通项公式;
}的通项公式;
(3)记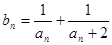 ,求数列{
,求数列{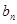 }的前n项和
}的前n项和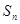 ,并证明
,并证明 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对数列 ,规定
,规定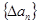 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中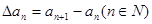 , 对自然数
, 对自然数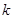 ,规定
,规定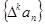 为
为 的
的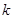 阶差分数列,其中
阶差分数列,其中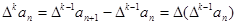 .
.
(1)已知数列 的通项公式
的通项公式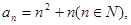 ,试判断
,试判断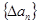 ,
,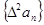 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列 首项
首项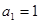 ,且满足
,且满足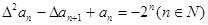 ,求数列
,求数列 的通项公式。
的通项公式。
(3)对(2)中数列 ,是否存在等差数列
,是否存在等差数列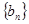 ,使得
,使得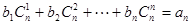 对一切自然
对一切自然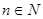 都成立?若存在,求数列
都成立?若存在,求数列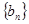 的通项公式;若不存在,则请说明理由。
的通项公式;若不存在,则请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律。下图是一个11阶杨辉三角:
(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14个数与第15个数的比为 ,求n的值;
,求n的值;
(3)求n阶(包括0阶)杨辉三角的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35。显然,1+3+6+10+15=35。事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数。试用含有m、k 的数学公式表示上述结论,并给予证明。
的数学公式表示上述结论,并给予证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com