
【题目】为调查市民对汽车品牌的认可度,在秋季车展上,从有意购车的500名市民中,随机抽样100名市民,按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2.频率分布表Ⅰ
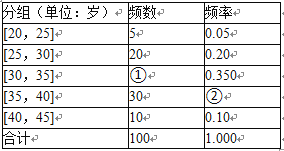
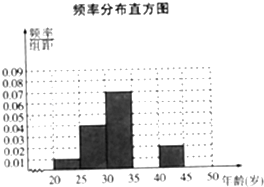
(1)频率分布表中的①②位置应填什么数?并补全频率分布直方图,再根据频率分布直方图统计这500名志愿者得平均年龄;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加的宣传活动,再从这20名中选取2名志愿者担任主要发言人.记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
【答案】(1)![]() ,
,![]() ,频率分布直方图见解析,
,频率分布直方图见解析,![]() 岁;(2)分布列见解析,
岁;(2)分布列见解析,![]() .
.
【解析】
试题分析:本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.第一问,利用频率分布表和频率分布直方图能求出频率分布表中的①②位置应填什么数,并补全频率分布直方图,再根据频率分布直方图能统计出这![]() 名志愿者得平均年龄;第二问,由表知抽取的
名志愿者得平均年龄;第二问,由表知抽取的![]() 人中,年龄低于
人中,年龄低于![]() 岁的有
岁的有![]() 人,故
人,故![]() 的可能取值为
的可能取值为![]() ,分别求出相应的概率,由此能求出
,分别求出相应的概率,由此能求出![]() 的分布列及数学期望.
的分布列及数学期望.
试题解析:(1)由题意知频率分布表中的①位置应填数字为:![]() ,
,
②位置应填数字为:![]() .
.
补全频率分布直方图,如图所示.

平均年龄估值为:![]() (岁).
(岁).
(2)由表知,抽取的![]() 人中,年龄低于
人中,年龄低于![]() 岁的有
岁的有![]() 人,故
人,故![]() 的可能取值为
的可能取值为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴X的分布列为:

![]() .
.


科目:高中数学 来源: 题型:
【题目】对于函数![]() 、
、![]() 、
、![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 、
、![]() 的和谐函数.
的和谐函数.
(1)已知函数![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 是否为
是否为![]() 、
、![]() 的和谐函数?并说明理由;
的和谐函数?并说明理由;
(2)已知![]() 为函数
为函数![]() ,
,![]() 的和谐函数,其中
的和谐函数,其中![]() ,若方程
,若方程![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)设一次订购量为![]() 个,零件的实际出厂单价为
个,零件的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5;4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(I)求取出的3个球编号都不相同的概率;
(II)记![]() 为取出的3个球中编号的最小值,求
为取出的3个球中编号的最小值,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com