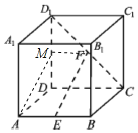
【题目】正方体ABCD-A1B1C1D1中，E为AB中点，F为CD1中点．
（1）求证：EF∥平面ADD1A1；
（2）求直线EF和平面CDD1C1所成角的正弦值．
【答案】（1）见解析；（2）
【解析】试题分析：（1）取DD1中点M，连接MA，MF，易得AEFM是平行四边形，有EF∥AM，从而得证；
（2）因为EF∥AM，AD⊥平面CDD1C1，所以∠AMD与直线EF和平面CDD1C1所成角相等，在Rt△AMD中求解即可.
试题解析：
（1）证明：取DD1中点M，连接MA，MF，有
，
所以AEFM是平行四边形，
所以EF∥AM，又AM平面ADD1A1，EF平面ADD1A1，
所以EF∥平面ADD1A1，得证．
（2）因为EF∥AM，AD⊥平面CDD1C1，所以∠AMD与直线EF和平面CDD1C1所成角相等，
又在Rt△AMD中，有
，所以直线EF和平面CDD1C1所成角的正弦值为
．
长江作业本同步练习册系列答案科目：高中数学 来源： 题型：
【题目】假设某种设备使用的年限x（年）与所支出的维修费用y（万元）有以下统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求：
（1）求
； （2）线性回归方程
；
（3）估计使用10年时，维修费用是多少？
附：利用“最小二乘法”计算a,b的值时,可根据以下公式：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
．
（1）求函数
的单调递增区间；
（2）当
时，方程
恰有两个不同的实数根，求实数
的取值范围；
（3）将函数的图象向右平移
个单位后所得函数
的图象关于原点中心对称，求
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法错误的是
A. 对分类变量X与Y，随机变量K2的观测值k越大，则判断“X与Y有关系”的把握程度越小
B. 在回归直线方程
=0.2x+0.8中，当解释变量x每增加1个单位时，预报变量
平均增加0.2个单位
C. 两个随机变量的线性相关性越强，则相关系数的绝对值就越接近于1
D. 回归直线过样本点的中心（
， 
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司即将推车一款新型智能手机，为了更好地对产品进行宣传，需预估市民购买该款手机是否与年龄有关，现随机抽取了50名市民进行购买意愿的问卷调查，若得分低于60分，说明购买意愿弱；若得分不低于60分，说明购买意愿强，调查结果用茎叶图表示如图所示.
（1）根据茎叶图中的数据完成
列联表，并判断是否有95%的把握认为市民是否购买该款手机与年龄有关？
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | |||
大于40岁 | |||
合计 |
（2）从购买意愿弱的市民中按年龄进行分层抽样，共抽取5人，从这5人中随机抽取2人进行采访，求这2人都是年龄大于40岁的概率.
附：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知A是椭圆E： 
=1的左顶点，斜率为k（k＞0）的直线交E与A，M两点，点N在E上，MA⊥NA．
（1）当|AM|=|AN|时，求△AMN的面积
（2）当2|AM|=|AN|时，证明： 
＜k＜2．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．
（1）证明MN∥平面PAB；
（2）求四面体N﹣BCM的体积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
