
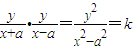 (y≠0),由AC,BC的斜率存在可知A≠90°,B≠90°
(y≠0),由AC,BC的斜率存在可知A≠90°,B≠90°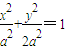 ,则C在在
,则C在在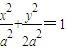 上,同时在圆x2+y2=a2(y≠0)外,从而可得C,而KAC•KBC<0可得直线AC的倾斜角为锐角,BC的倾斜角为钝角,可判断B,A
上,同时在圆x2+y2=a2(y≠0)外,从而可得C,而KAC•KBC<0可得直线AC的倾斜角为锐角,BC的倾斜角为钝角,可判断B,A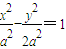 ,同②可得C≠90°,由KAC•KBC>0,根据两直线的倾斜角可判断A,B
,同②可得C≠90°,由KAC•KBC>0,根据两直线的倾斜角可判断A,B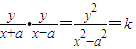 (y≠0)
(y≠0)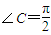
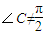 ,A≠90°,B≠90°
,A≠90°,B≠90°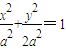 ,而x2+y2=a2(y≠0),则C在在
,而x2+y2=a2(y≠0),则C在在 上,同时在圆x2+y2=a2(y≠0)外,从而可得C<90°,而KAC•KBC<0可得直线AC的倾斜角为锐角,BC的倾斜角为钝角,故可得B<90°,A<90°
上,同时在圆x2+y2=a2(y≠0)外,从而可得C<90°,而KAC•KBC<0可得直线AC的倾斜角为锐角,BC的倾斜角为钝角,故可得B<90°,A<90°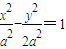 ,同②可得C≠90°,但由KAC•KBC>0可得两直线的倾斜角同时为锐角(或钝角)从而可得A,B中有一个锐角一个钝角
,同②可得C≠90°,但由KAC•KBC>0可得两直线的倾斜角同时为锐角(或钝角)从而可得A,B中有一个锐角一个钝角

 作业辅导系列答案
作业辅导系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com