练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法正确的是（ ）

    A.若等比数列的前项和为，则，，也成等比数列.

    B.命题“若为的极值点，则”的逆命题是真命题．

    C.“为真命题”是“为真命题”的充分不必要条件．

    D.命题“，使得”的否定是：“，”．

    【答案】C

    【解析】

    举反例，判断AB选项；由且命题和或命题的性质判断C选项；由特称命题的否定的定义判断D选项.

    对于A项，设，则，此数列不是等比数列，故A错误；

    对于B项，设，，但是不是极值点，故B错误；

    为真命题，则都为真命题，推出为真命题；

    对于C项，反过来，为真命题，则中至少有一个为真命题，不一定推出为真命题，即“为真命题”是“为真命题”的充分不必要条件，故C正确；

    对于D项，命题“，使得”的否定是“，”，故D错误.

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】陆良县2017届和2018届都取得了辉煌的成绩，两年均有人考入清华大学或北京大学，600分以上的考生进一步创历史新高.对此北辰中学某学习兴趣小组对2019届20名学生的数学成绩进行了调查，所得分数分组为，，，，，据此制作的频率分布直方图如图所示.

    （1）求出直方图中的值；

    （2）利用直方图估计2019届20名学生分数的众数和中位数（同一组中的数据用该组区间的中点值作代表）；

    （3）若从分数在的学生中，随机的抽取2名学生进行辅导，求抽到的学生来自同一组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国古代典籍《周易》用“卦”描述万物的变化，每一卦由六爻组成.其中有一种起卦方法称为“金钱起卦法”，其做法为：取三枚相同的钱币合于双手中，上下摇动数下使钱币翻滚摩擦，再随意抛撒钱币到桌面或平盘等硬物上，如此重复六次，得到六爻.若三枚钱币全部正面向上或全部反面向上，就称为变爻.若每一枚钱币正面向上的概率为，则一卦中恰有两个变爻的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

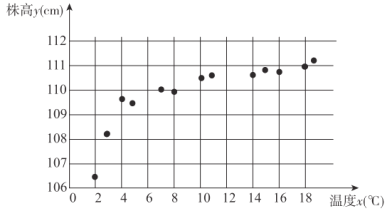
    【题目】一种室内种植的珍贵草药的株高(单位:)与一定范围内的温度(单位:)有关，现收集了该种草药的13组观测数据，得到如下的散点图，现根据散点图利用或建立关于的回归方程,令,,得到如下数据,且与()的相关系数分别为,且.

    10.15

    109.94

    3.04

    0.16

    （1）用相关系数说明哪种模型建立与的回归方程更合适;

    （2）根据（1）的结果及表中数据,建立关于的回归方程;

    （3）已知这种草药的利润与,的关系为，当为何值时，利润的预报值最大.

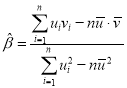    附:参考公式和数据:对于一组数据（）,其回归直线的斜率和截距的最小二乘估计分别为,,相关系数 ,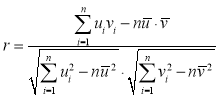

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“共享单车”的出现，为我们提供了一种新型的交通方式。某机构为了调查人们对此种交通方式的满意度，从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户，得到了一个用户满意度评分的样本，并绘制出茎叶图如图：

    （1）根据茎叶图，比较两城市满意度评分的平均值的大小及方差的大小（不要求计算出具体值，给出结论即可）；

    （2）若得分不低于80分，则认为该用户对此种交通方式“认可”，否则认为该用户对此种交通方式“不认可”，请根据此样本完成此2×2列联表，并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关；

    A

    B

    合计

    认可

    不认可

    合计

    （3）在A，B城市对此种交通方式“认可”的用户中按照分层抽样的方法抽取6人，若在此6人中推荐2人参加“单车维护”志愿活动，求A城市中至少有1人的概率。

    参考数据如下：（下面临界值表供参考）

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （参考公式，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正方形的边长为2，分别以，为一边在空间中作正三角形，，延长到点，使，连接，．

    （1）证明：平面；

    （2）求点到平面的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】足球是当今世界传播范围最广、参与人数最多的体育运动，具有广泛的社会影响，深受世界各国民众喜爱．

    （1）为调查大学生喜欢足球是否与性别有关，随机选取50名大学生进行问卷调查，当问卷评分不低于80分则认为喜欢足球，当评分低于80分则认为不喜欢足球，这50名大学生问卷评分的结果用茎叶图表示如图：

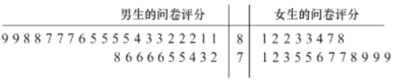
    请依据上述数据填写如下列联表：

    喜欢足球

    不喜欢足球

    总计

    女生

    男生

    总计

    请问是否有 的把握认为喜欢足球与性别有关？

    参考公式及数据：，．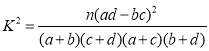

    0.100

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    （2）已知某国“糖果盒”足球场每年平均上座率与该国成年男子国家足球队在国际足联的年度排名线性相关，数据如表，，，

    年度排名

    9

    6

    3

    平均上座率

    0.9

    0.91

    0.92

    0.93

    0.95

    求变量与的线性回归方程，并预测排名为1时该球场的上座率．

    参考公式及数据：，；．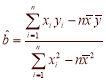

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分13分，（Ⅰ）小问5分，（Ⅱ）小问8分.）

    甲、乙、丙三人按下面的规则进行乒乓球比赛：第一局由甲、乙参加而丙轮空，以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为，且各局胜负相互独立.求：（Ⅰ）打满3局比赛还未停止的概率；（Ⅱ）比赛停止时已打局数的分别列与期望E．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在统计调查中，问卷的设计是一门很大的学问，特别是对一些敏感性问题.例如学生在考试中有无作弊现象，社会上的偷税漏税等.更要精心设计问卷.设法消除被调查者的顾虑，使他们能够如实回答问题，否则被调查者往往会拒绝冋答，或不提供真实情况，为了调查中学生中的早恋现象，随机抽出300名学生，调查中使用了两个问題.①你的学籍号的最后一位数是奇数（学籍号的后四位是序号）；②你是否有早恋现象，让被调查者从装有4个红球，6个黑球（除颜色外完全相同）的袋子中随机摸取两个球.摸到两球同色的学生如实回答第一个问题，摸到两球异色的学生如实回答第二个问题，回答“是”的人往一个盒子中放一个小石子，回答“否”的人什么都不放，后来在盒子中收到了78个小石子.

    （1）你能否估算出中学生早恋人数的百分比？

    （2）若从该地区中学生中随机抽取一个班（40人），设其中恰有个人存在早恋的现象，求的分布列及数学期望.

    查看答案和解析>>

    同步练习册答案