
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,将
,将![]() 的图像向右平移
的图像向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() ,
,![]() 的图像关于
的图像关于![]() 轴对称,且
轴对称,且![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,若函数
,若函数![]() 的图像在
的图像在![]() 上恰有2个最高点,求实数
上恰有2个最高点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据给出的周期,可求出ω的值;由f(x)的图象向右平移![]() 个单位长度,函数的图象关于y轴对称,求出φ的值;由
个单位长度,函数的图象关于y轴对称,求出φ的值;由![]() ,得A的值即可;
,得A的值即可;
(2)由(1)可得F(x)的解析式,由辅助角公式进行化简,利用函数图象分析即可得出结果.
(1)∵函数![]() 的最小正周期为π,
的最小正周期为π,
∴π![]() ,解得ω=2,
,解得ω=2,
∵g(x)=f(x![]() )=Acos[2(x
)=Acos[2(x![]() )+φ]=Acos(2x
)+φ]=Acos(2x![]() φ),且g(x)的图象关于y轴对称,
φ),且g(x)的图象关于y轴对称,
∴![]() φ=kπ,k∈Z,即φ=kπ
φ=kπ,k∈Z,即φ=kπ![]() ,k∈Z,
,k∈Z,
∴由|φ|![]() ,可得φ
,可得φ![]() ,可得f(x)=Acos(2x
,可得f(x)=Acos(2x![]() ),
),
∵![]() ,即f(
,即f(![]() )=Acos[2×(
)=Acos[2×(![]() )
)![]() ]=Acos0=A=2,
]=Acos0=A=2,
∴函数f(x)的解析式为![]() .
.
(2)由(1)知g(x)=2cos2x;
F(x)=2cos(2x![]() )+2cos2x=2(cos2xcos
)+2cos2x=2(cos2xcos![]() sin2xsin
sin2xsin![]() )+2cos2x=3cos2x
)+2cos2x=3cos2x![]() sin2x,
sin2x,
=2![]() cos(2x
cos(2x![]() );
);
∵x∈[0,aπ](a>0);
∴2x![]() ∈[
∈[![]() ,2aπ
,2aπ![]() ];
];
∵函数F(x)的图象在x∈[0,aπ](a>0)上恰有2个最高点;
∴结合余弦函数的图象(如图示)知,4π≤2πa![]() 6π;
6π;
故解得a∈![]()
故实数a的取值范围为![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 是它的上顶点,点
是它的上顶点,点![]() 各不相同且均在椭圆上.
各不相同且均在椭圆上.
(1)若![]() 恰为椭圆长轴的两个端点,求
恰为椭圆长轴的两个端点,求![]() 的面积;
的面积;
(2)若![]() ,求证:直线
,求证:直线![]() 过一定点;
过一定点;
(3)若![]() ,
,![]() 的外接圆半径为
的外接圆半径为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元,顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克,需要支付180元,则x=________;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
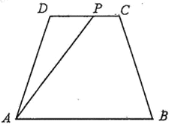
【题目】如图:已知某公园的四处景观分别位于等腰梯形![]() 的四个顶点处,其中
的四个顶点处,其中![]() ,
,![]() 两地的距离为
两地的距离为![]() 千米,
千米,![]() ,
,![]() 两地的距离为
两地的距离为![]() 千米,
千米,![]() .现拟规划在
.现拟规划在![]() (不包括端点)路段上增加一个景观
(不包括端点)路段上增加一个景观![]() ,并建造观光路直接通往
,并建造观光路直接通往![]() 处,造价为每千米
处,造价为每千米![]() 万元,又重新装饰
万元,又重新装饰![]() 路段,造价为每千米
路段,造价为每千米![]() 万元.
万元.
(1)若拟修建观光路![]() 路段长为
路段长为![]() 千米,求
千米,求![]() 路段的造价;
路段的造价;
(2)设![]() ,当
,当![]() 为何值时,
为何值时,![]() ,
,![]() 段的总造价最低.
段的总造价最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]() ,
,![]() 为异面直线; ②若
为异面直线; ②若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,则
,则![]() ; ④若
; ④若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
则上述命题中真命题的序号为( )
A.①②B.③④C.②D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任意一点,点
上任意一点,点![]() 关于原点
关于原点![]() 的对称点为点
的对称点为点![]() ,有
,有![]() ,且当
,且当![]() 的面积最大时为等边三角形.
的面积最大时为等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)与圆![]() 相切的直线
相切的直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,若椭圆上存在点
两点,若椭圆上存在点![]() 满足
满足![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com