
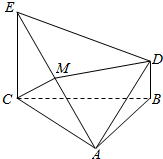
 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.分析 (Ⅰ)取AC的中点N,连接MN,BN,利用三角形中位线定理与平行四边形的判定与性质定理可得DM∥BN,再利用线面平行的判定定理可得:DM∥平面ABC.
(Ⅱ)先证明DM⊥平面ACE,从而证出CM⊥平面ADE,进而证出CM⊥DE.
解答  证明:(Ⅰ)如图示:取AC的中点N,连接MN,BN
证明:(Ⅰ)如图示:取AC的中点N,连接MN,BN
∵M是AE的中点,∴MN∥CE,CE=2MN,
∵CE∥BD,CE=2BD,
∴MN∥BD,MN=BD
∴四边形BDMN为平行四边形,
∴DM∥BN,DM?平面ABC,BN?平面ABC,
∴DM∥平面ABC.
(Ⅱ)∵BN⊥AC,BN⊥MN,AC∩MN=N,
∴BN⊥平面ACE,
∵DM∥BN,∴DM平面ACE,
∴CM⊥DM,而CM⊥AE,DM∩AE=M,
∴CM⊥平面ADE,
∴CM⊥DE.
点评 本题考查了线面平行的判定定理、三角形的中位线定理、平行四边形的判定与性质定理,考查了推理能力与计算能力,属于中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3.60.8>log0.40.5>2.40.8>log0.34.2 | |
| B. | 3.60.8>2.40.8>log0.34.2>log0.40.5 | |
| C. | log0.40.5>2.40.8>3.60.8log0.34.2 | |
| D. | 3.60.8>2.40.8>log0.40.5>log0.34.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2y-3)2=12x | B. | (2y+3)2=12x | C. | (2y-3)2=-12x | D. | (2y+3)2=-12x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com