
ЁОЬтФПЁПЁАДѓжкДДвЕЃЌЭђжкДДаТЁБЪЧРюПЫЧПзмРэдкБОНьеўИЎЙЄзїБЈИцжаЯђШЋЙњШЫУёЗЂГіЕФПкКХ.ФГЩњВњЦѓвЕЛ§МЋЯьгІКХейЃЌДѓСІбаЗЂаТВњЦЗЃЌЮЊСЫЖдаТбаЗЂЕФвЛХњВњЦЗНјааКЯРэЖЈМлЃЌНЋИУВњЦЗАДЪТЯШФтЖЈЕФМлИёНјааЪдЯњЃЌЕУЕНвЛзщЯњЪлЪ§Он![]()
![]() ЃЌШчБэЫљЪОЃК
ЃЌШчБэЫљЪОЃК
ЪдЯњЕЅМл | 4 | 5 | 6 | 7 | 8 | 9 |
ВњЦЗЯњСП | q | 84 | 83 | 80 | 75 | 68 |
вбжЊ![]() ЃЌ
ЃЌ![]() .
.
ЃЈЂёЃЉЧѓГі![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂђЃЉвбжЊБфСП![]() ЃЌ
ЃЌ![]() ОпгаЯпадЯрЙиЙиЯЕЃЌЧѓВњЦЗЯњСП
ОпгаЯпадЯрЙиЙиЯЕЃЌЧѓВњЦЗЯњСП![]() ЃЈМўЃЉЙигкЪдЯњЕЅМл
ЃЈМўЃЉЙигкЪдЯњЕЅМл![]() ЃЈдЊЃЉЕФЯпадЛиЙщЗНГЬ
ЃЈдЊЃЉЕФЯпадЛиЙщЗНГЬ![]() ЃЛ
ЃЛ
ЃЈЂѓЃЉгУ![]() БэЪОгУЃЈЂђЃЉжаЫљЧѓЕФЯпадЛиЙщЗНГЬЕУЕНЕФгы
БэЪОгУЃЈЂђЃЉжаЫљЧѓЕФЯпадЛиЙщЗНГЬЕУЕНЕФгы![]() ЖдгІЕФВњЦЗЯњСПЕФЙРМЦжЕ.ЕБЯњЪлЪ§Он
ЖдгІЕФВњЦЗЯњСПЕФЙРМЦжЕ.ЕБЯњЪлЪ§Он![]() ЖдгІЕФВаВюЕФОјЖджЕ
ЖдгІЕФВаВюЕФОјЖджЕ![]() ЪБЃЌдђНЋЯњЪлЪ§Он
ЪБЃЌдђНЋЯњЪлЪ§Он![]() ГЦЮЊвЛИіЁАКУЪ§ОнЁБ.ЯжДг6ИіЯњЪлЪ§ОнжаШЮШЁ2ИіЃЌЧѓЁАКУЪ§ОнЁБжСЩйгавЛИіЕФИХТЪ.
ГЦЮЊвЛИіЁАКУЪ§ОнЁБ.ЯжДг6ИіЯњЪлЪ§ОнжаШЮШЁ2ИіЃЌЧѓЁАКУЪ§ОнЁБжСЩйгавЛИіЕФИХТЪ.
ЃЈВЮПМЙЋЪНЃКЯпадЛиЙщЗНГЬжа![]() ЃЌ
ЃЌ![]() ЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ
ЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЛЃЈЂђЃЉ
ЃЛЃЈЂђЃЉ![]() ЃЛЃЈЂѓЃЉ
ЃЛЃЈЂѓЃЉ![]()
ЁОНтЮіЁП
ЃЈЂёЃЉРћгУЦНОљЪ§ЧѓГі![]() МДПЩЃЛ
МДПЩЃЛ
ЃЈЂђЃЉВЮПМЙЋЪНЧѓНтЯпадЛиЙщЗНГЬМДПЩЕУНтЃЛ
ЃЈЂѓЃЉНсКЯЃЈЂђЃЉЃЌТњзу![]()
![]() ЕФЙВга3ИіЁАКУЪ§ОнЁБЃЌгжДг6ИіЯњЪлЪ§ОнжаШЮШЁ2ИіЃЌЙВга
ЕФЙВга3ИіЁАКУЪ§ОнЁБЃЌгжДг6ИіЯњЪлЪ§ОнжаШЮШЁ2ИіЃЌЙВга![]() жжВЛЭЌЕФШЁЗЈЃЌРћгУИХТЪЙЋЪНдЫЫуМДПЩ.
жжВЛЭЌЕФШЁЗЈЃЌРћгУИХТЪЙЋЪНдЫЫуМДПЩ.
ЃЈЂёЃЉ![]() ЃЌПЩЧѓЕУ
ЃЌПЩЧѓЕУ![]() .
.
ЃЈЂђЃЉ ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЫљвдЫљЧѓЕФЯпадЛиЙщЗНГЬЮЊ![]() .
.
ЃЈЂѓЃЉРћгУЃЈЂђЃЉжаЫљЧѓЕФЯпадЛиЙщЗНГЬ![]() ПЩЕУЃЌЕБ
ПЩЕУЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() .
.
гыЯњЪлЪ§ОнЖдБШПЩжЊТњзу![]()
![]() ЕФЙВга3ИіЁАКУЪ§ОнЁБЃК
ЕФЙВга3ИіЁАКУЪ§ОнЁБЃК![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() .
.
гжДг6ИіЯњЪлЪ§ОнжаШЮШЁ2ИіЃЌЙВга![]() =15жжВЛЭЌЕФШЁЗЈЃЌ
=15жжВЛЭЌЕФШЁЗЈЃЌ
ЩшЫљЧѓЪТМўгУ![]() БэЪО ЃЌдђ
БэЪО ЃЌдђ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮ![]() ЕФБпГЄЮЊ
ЕФБпГЄЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгк
НЛгк![]() ЕуЃЎНЋСтаЮ
ЕуЃЎНЋСтаЮ![]() биЖдНЧЯп
биЖдНЧЯп![]() елЦ№ЃЌЕУЕНШ§РтзЖ
елЦ№ЃЌЕУЕНШ§РтзЖ![]() ЃЌЕу
ЃЌЕу![]() ЪЧРт
ЪЧРт![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЎ
ЃЎ
ЃЈIЃЉЧѓжЄЃКЦНУц![]() ЁЭЦНУц
ЁЭЦНУц![]() ЃЛ
ЃЛ
ЃЈIIЃЉЧѓЖўУцНЧ![]() ЕФгрЯвжЕЃЎ
ЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃК
ЃК
ЃЈ1ЃЉШє![]() ЃЌЧѓyЃНfЃЈxЃЉЕФзюДѓжЕКЭзюаЁжЕЃЌВЂаДГіЯргІЕФxжЕЃЛ
ЃЌЧѓyЃНfЃЈxЃЉЕФзюДѓжЕКЭзюаЁжЕЃЌВЂаДГіЯргІЕФxжЕЃЛ
ЃЈ2ЃЉНЋКЏЪ§yЃНfЃЈxЃЉЕФЭМЯѓЯђгвЦНвЦ![]() ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛЃЌЕУЕНКЏЪ§yЃНgЃЈxЃЉЕФЭМЯѓЃЌЧјМф[aЃЌb]ЃЈaЃЌbЁЪRЧвaЃМbЃЉТњзуЃКyЃНgЃЈxЃЉдк[aЃЌb]ЩЯжСЩйКЌга20ИіСуЕуЃЌдкЫљгаТњзуЩЯЪіЬѕМўЕФ[aЃЌb]жаЃЌЧѓbЉaЕФзюаЁжЕЃЎ
ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛЃЌЕУЕНКЏЪ§yЃНgЃЈxЃЉЕФЭМЯѓЃЌЧјМф[aЃЌb]ЃЈaЃЌbЁЪRЧвaЃМbЃЉТњзуЃКyЃНgЃЈxЃЉдк[aЃЌb]ЩЯжСЩйКЌга20ИіСуЕуЃЌдкЫљгаТњзуЩЯЪіЬѕМўЕФ[aЃЌb]жаЃЌЧѓbЉaЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§f(x)=ax2ЈCaЈClnxЃЌg(x)=![]() ЃЌЦфжаaЁЪRЃЌe=2.718ЁЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЃЌЦфжаaЁЪRЃЌe=2.718ЁЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЃЈ1ЃЉЬжТлf(x) ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉжЄУїЃКЕБxЃО1ЪБЃЌg(x)ЃО0ЃЛ
ЃЈ3ЃЉШчЙћf(x)ЃОg(x) дкЧјМфЃЈ1ЃЌ+ЁоЃЉФкКуГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
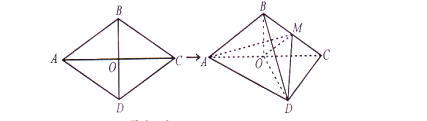
ЁОЬтФПЁПдкЫФРтзЖ![]() жаЃЌ
жаЃЌ![]() ЦНУц
ЦНУц![]() ЃЌЧвЕзУц
ЃЌЧвЕзУц![]() ЮЊБпГЄЮЊ2ЕФСтаЮЃЌ
ЮЊБпГЄЮЊ2ЕФСтаЮЃЌ![]() ,
,![]() .
.
ЃЈЂёЃЉМЧ![]() дкЦНУц
дкЦНУц![]() ФкЕФЩфгАЮЊ
ФкЕФЩфгАЮЊ![]() ЃЈМД
ЃЈМД![]() ЦНУц
ЦНУц![]() ЃЉЃЌЪдгУзїЭМЕФЗНЗЈевГіMЕуЮЛжУЃЌВЂаДГі
ЃЉЃЌЪдгУзїЭМЕФЗНЗЈевГіMЕуЮЛжУЃЌВЂаДГі![]() ЕФГЄЃЈвЊЧѓаДГізїЭМЙ§ГЬЃЌВЂБЃСєзїЭМКлМЃЃЌВЛашжЄУїЙ§ГЬКЭМЦЫуЙ§ГЬЃЉЃЛ
ЕФГЄЃЈвЊЧѓаДГізїЭМЙ§ГЬЃЌВЂБЃСєзїЭМКлМЃЃЌВЛашжЄУїЙ§ГЬКЭМЦЫуЙ§ГЬЃЉЃЛ

ЃЈЂђЃЉЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈЃК
ЂйУќЬтЃКЁАдк![]() жаЃЌШє
жаЃЌШє![]() дђ
дђ![]() ЁБЕФФцУќЬтЮЊМйУќЬтЃЛ
ЁБЕФФцУќЬтЮЊМйУќЬтЃЛ
ЂкЁА![]() ЁБЪЧжБЯп
ЁБЪЧжБЯп![]() гыдВ
гыдВ![]() ЯрНЛЕФГфЗжВЛБивЊЬѕМўЃЛ
ЯрНЛЕФГфЗжВЛБивЊЬѕМўЃЛ
ЂлУќЬтЃКЁАШє![]() дђ
дђ![]() ЁБЕФФцЗёУќЬтЪЧЁАШє
ЁБЕФФцЗёУќЬтЪЧЁАШє![]() дђ
дђ![]() ЁБЃЛ
ЁБЃЛ
ЂмШє![]() Лђ
Лђ![]() ЃЌдђ
ЃЌдђ![]() ЮЊецУќЬтЁЃ
ЮЊецУќЬтЁЃ
Цфжае§ШЗЕФЫЕЗЈИіЪ§ЮЊЃЈЃЉ
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩш![]() ЮЊЦцКЏЪ§,
ЮЊЦцКЏЪ§,![]() ЮЊГЃЪ§.
ЮЊГЃЪ§.
ЃЈ1ЃЉЧѓ![]() ЕФжЕ
ЕФжЕ
ЃЈ2ЃЉХаЖЯКЏЪ§![]() дк
дк![]() ЩЯЕФЕЅЕїад,ВЂЫЕУїРэгЩ;
ЩЯЕФЕЅЕїад,ВЂЫЕУїРэгЩ;
ЃЈ3ЃЉШєЖдгкЧјМф![]() ЩЯЕФУПвЛИі
ЩЯЕФУПвЛИі![]() жЕ,ВЛЕШЪН
жЕ,ВЛЕШЪН![]() КуГЩСЂ,ЧѓЪЕЪ§
КуГЩСЂ,ЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЉзїХзЮяЯп
ЮЊГЃЪ§ЃЉзїХзЮяЯп![]() ЕФСНЬѕЧаЯпЃЌЧаЕуЗжБ№ЮЊ
ЕФСНЬѕЧаЯпЃЌЧаЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЙ§НЙЕуЧвдк![]() жсЩЯНиОрЮЊ
жсЩЯНиОрЮЊ![]() ЕФжБЯп
ЕФжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌ
СНЕуЃЌ![]() ЃЌ
ЃЌ![]() СНЕудк
СНЕудк![]() жсЩЯЕФЩфгАЗжБ№ЮЊ
жсЩЯЕФЩфгАЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓХзЮяЯп
ЃЌЧѓХзЮяЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшжБЯп![]() ЃЌ
ЃЌ![]() ЕФаБТЪЗжБ№ЮЊ
ЕФаБТЪЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() .ЧѓжЄЃК
.ЧѓжЄЃК![]() ЮЊЖЈжЕ.
ЮЊЖЈжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЫљбЇаЃНјааЭЌвЛУХПЮГЬЕФПМЪдЃЌАДеебЇЩњПМЪдГЩМЈгХауКЭВЛгХауЭГМЦГЩМЈКѓЃЌЕУЕНШчЯТ![]() СаСЊБэЃК
СаСЊБэЃК
АрМЖгыГЩМЈСаСЊБэ
гХау | ВЛгХау | змМЦ | |
МзЖг | 80 | 40 | 120 |
ввЖг | 240 | 200 | 240 |
КЯМЦ | 320 | 240 | 560 |
ЃЈ1ЃЉФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.025ЕФЧАЬсЯТШЯЮЊГЩМЈгыбЇаЃгаЙиЯЕЃЛ
ЃЈ2ЃЉВЩгУЗжВуГщбљЕФЗНЗЈдкСНЫљбЇаЃГЩМЈгХауЕФ320УћбЇЩњжаГщШЁ16УћЭЌбЇЃЎЯжДгет16УћЭЌбЇжаЫцЛњГщШЁ3УћдЫЭЌбЇзїЮЊГЩМЈгХаубЇЩњДњБэНщЩмбЇЯАОбщЃЌМЧет3УћЭЌбЇРДздМзбЇаЃЕФШЫЪ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСагыЪ§бЇЦкЭћЃЎИНЃК
ЕФЗжВМСагыЪ§бЇЦкЭћЃЎИНЃК
ВЮПМЪ§ОнЃК
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЃЌЦфжа
ЃЌЦфжа![]() .
.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com