
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,短轴长和焦距都等于2,
轴上,短轴长和焦距都等于2, ![]() 是椭圆上的一点,且
是椭圆上的一点,且![]() 在第一象限内,过
在第一象限内,过![]() 且斜率等于
且斜率等于![]() 的直线与椭圆
的直线与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.

(Ⅰ)证明:直线![]() 的斜率为定值;
的斜率为定值;
(Ⅱ)求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() .
.
(1)求以右焦点为圆心,与双曲线![]() 的渐近线相切的圆的方程;
的渐近线相切的圆的方程;
(2)若经过点![]() 的直线与双曲线
的直线与双曲线![]() 的右支交于不同两点
的右支交于不同两点![]() 、
、![]() ,求线段
,求线段![]() 的中垂线
的中垂线![]() 在
在![]() 轴上截距
轴上截距![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且a+b+c=8.
(1)若a=2,b=![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2![]() +sinB·cos2
+sinB·cos2![]() =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S=![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4 — 4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为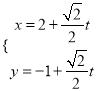 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(1)分别写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位安排7位员工对一周的7个夜晚值班,每位员工值一个夜班且不重复值班,其中员工甲必须安排在星期一或星期二值班,员工乙不能安排在星期二值班,员工丙必须安排在星期五值班,则这个单位安排夜晚值班的方案共有( )
A. 96种B. 144种C. 200种D. 216种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为庆祝成立二十周年,特举办《快乐大闯关》竞技类有奖活动,该活动共有四关,由两名男职员与两名女职员组成四人小组,设男职员闯过一至四关概率依次是![]() ,女职员闯过一至四关的概率依次是
,女职员闯过一至四关的概率依次是![]()
(1)求女职员闯过四关的概率;
(2)设![]() 表示四人小组闯过四关的人数,求随机变量
表示四人小组闯过四关的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“日行一万步,健康你一生”的养生观念已经深入人心,由于研究性学习的需要,某大学生收集了手机“微信运动”团队中特定甲、乙两个班级![]() 名成员一天行走的步数,然后采用分层抽样的方法按照
名成员一天行走的步数,然后采用分层抽样的方法按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 分层抽取了20名成员的步数,并绘制了如下尚不完整的茎叶图(单位:千步):
分层抽取了20名成员的步数,并绘制了如下尚不完整的茎叶图(单位:千步):

已知甲、乙两班行走步数的平均值都是44千步.
(1)求![]() 的值;
的值;
(2)(ⅰ)若![]() ,求甲、乙两个班级100名成员中行走步数在
,求甲、乙两个班级100名成员中行走步数在![]() ,
, ![]() ,
, ![]() ,
, ![]() 各层的人数;
各层的人数;
(ⅱ)若估计该团队中一天行走步数少于40千步的人数比处于![]() 千步的人数少12人,求
千步的人数少12人,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com