
����Ŀ��ijѧУ�����꼶��ѧ��500�ˣ���������300�ˣ�Ů��200�ˣ�Ϊ���о�ѧ������ѧ�ɼ��Ƿ����Ա��йأ��ֲ��÷ֲ�����ķ��������г�ȡ��100��ѧ������ͳ�����������п��Ե���ѧ������Ȼ���Ա��Ϊ�С�Ů���飬�ٽ�����ѧ���ķ����ֳ�5�飺[100��110����[110��120����[120��130����[130��140����[140��150]�ֱ����ͳ�ƣ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�� 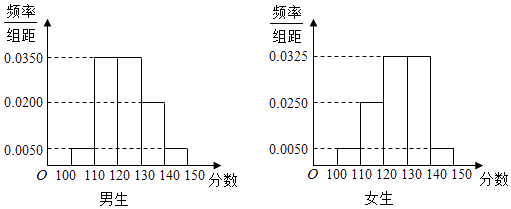
����K2= ![]() ��
��
��1���������з���С��110�ֵ�ѧ���������ȡ2�ˣ�������ǡ��Ϊһ��һŮ�ĸ��ʣ�
��2�����涨������С��130�ֵ�ѧ��Ϊ����ѧ�������������������֪�������2��2�����������ж��Ƿ���90%�İ�����Ϊ����ѧ���������Ա��йء���
P��K2��k0�� | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
���𰸡�
��1���⣺����֪�ã���ȡ��100��ѧ���У�����60����Ů��40����
����С�ڵ���110�ֵ�ѧ���У�
��������60��0.05=3���ˣ�����ΪA1��A2��A3��
Ů����40��0.05=2���ˣ�����ΪB1��B2������2�֣�
���������ȡ2��ѧ�������еĿ��ܽ������10�֣������ǣ�
��A1��A2������A1��A3������A2��A3������A1��B1������A1��B2����
��A2��B1������A2��B2������A3��B1������A3��B2������B1��B2����
���У�����ѧ��ǡ��Ϊһ��һŮ�Ŀ��ܽ������6�֣������ǣ�
��A1��B1������A1��B2������A2��B1����
��A2��B2������A3��B1������A3��B2����
������ĸ���ΪP= ![]() =
= ![]() ��
��
��2���⣺��Ƶ�ʷֲ�ֱ��ͼ��֪��
�ڳ�ȡ��100��ѧ���У����� 60��0.25=15���ˣ���Ů��40��0.375=15���ˣ�
�ݴ˿ɵ�2��2���������£�
��ѧ������ | ����ѧ������ | �ϼ� | |
���� | 15 | 45 | 60 |
�� | 15 | 25 | 40 |
�ϼ� | 30 | 70 | 100 |
���Ե�K2= ![]() =
= ![]() ��1.79��
��1.79��
��Ϊ1.79��2.706��
����û��90%�İ�����Ϊ����ѧ���������Ա��йء�
����������1�����ݷֲ����ԭ�������ȡ���С�Ů�������������оٷ���������¼����������Ӧ�ĸ���ֵ����2����Ƶ�ʷֲ�ֱ��ͼ�����Ӧ�����ݣ���д������������K2ֵ�������������ɵó����ʽ��ۣ�
�����㾫����������Ĺؼ���������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��


 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x���Ƕ�����R�ϵĺ�����������ʵ��m��n������f��m��f��n��=f��m+n�����ҵ�x��0ʱ��0��f��x����1��
��1��֤������f��0��=1���ڵ�x��0ʱ��f��x����1����f��x����R�ϵ���������
��2����a��R���Խ����x�IJ���ʽf��x2��3ax+1��f����3x+6a+1����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��2��a����x��1����2lnx��g��x��= ![]() ��a��R��eΪ��Ȼ�����ĵ�����
��a��R��eΪ��Ȼ�����ĵ�����
����a=1ʱ����f��x���ĵ������䣻
����������f��x����![]() ������㣬��a����Сֵ��
������㣬��a����Сֵ��
�����������������x0�ʣ�0��e]���ڣ�0��e]���ܴ���������ͬ��xi��i=1��2����ʹ��f��xi��=g��x0����������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=2cos2x+ ![]() sin2x��1��
sin2x��1��
��1����f��x�������ֵ����ʱ��xֵ
��2����f��x���ĵ���������
��3����x��[�� ![]() ��
�� ![]() ]ʱ����f��x����ֵ��
]ʱ����f��x����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�߲˻�����ֲ���������������г������֪���Ӷ���һ�����300���ڣ����������ۼ�������ʱ��Ĺ�ϵ��ͼһ��һ�����߱�ʾ������������ֲ�ɱ�������ʱ��Ĺ�ϵ��ͼ���������߶α�ʾ�� 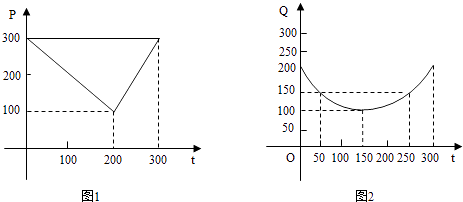
��1��д��ͼһ��ʾ���г��ۼ���ʱ��ĺ�����ϵʽp=f��t����д��ͼ����ʾ����ֲ�ɱ���ʱ��ĺ�����ϵʽQ=g��t����
��2���϶��г��ۼۼ�ȥ��ֲ�ɱ�Ϊ�����棬�ʺ�ʱ���е����������������ע���г��ۼ۸���ֲ�ɱ��ĵ�λ��Ԫ/102�K��ʱ�䵥λ���죩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊ��ǿ����Ļ���������ʶ������ȫ��������������־Ը�ߣ��ִӷ���������־Ը���������ȡ100����������飺��1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��
����4��![]() ����5��
����5��![]() ���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��

��1���ֱ����3��4��5���Ƶ�ʣ�
��2�����ӵ�3��4��5�����÷ֲ�����ķ�����ȡ6��־Ը�߲μӹ㳡�������Ӧ�ӵ�3��4��5�����ȡ������־Ը�ߣ�
��3���ڣ�2���������£����о�������6��־Ը���������ȡ2��־Ը�߽����������飬���4��������һ��־Ը�߱����еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪p������x2��mx��1��0����������ȵĸ�����q������4x2��4(m��2)x��1��0��ʵ������p��qΪ�棬p��qΪ�٣���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() =1��a��b��0����������Ϊ
=1��a��b��0����������Ϊ ![]() ��A��a��0����B��0��b����O��0��0������OAB�����Ϊ4��
��A��a��0����B��0��b����O��0��0������OAB�����Ϊ4��
��1������Բ�ı�����
��2����ֱ��l��y=kx+1����ԲC�ཻ��P��Q���㣬�Ƿ����������ʵ��k��ʹ����PQΪֱ����Բ��ԭ�㣬�����ڣ������k��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P��ABCD������ABCD��ֱ�����Σ�AD��BC����BCD=90�㣬PA�͵���ABCD����ABM�DZ߳�Ϊ2�ĵȱ������Σ� ![]() ��
��
������֤��ƽ��PAM��ƽ��PDM��
��������EΪPC�е㣬������P��MD��E������ֵ��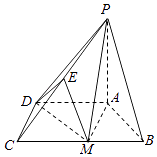
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com