
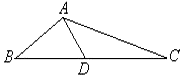
 如图所示,在△ABC中,AB=3$\sqrt{6},B=\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$
如图所示,在△ABC中,AB=3$\sqrt{6},B=\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$分析 (Ⅰ)在△ABD中,由已知利用正弦定理即可计算得解BD的值.
(Ⅱ)由已知利用正弦定理可求AD的值,在△ACD中,由余弦定理可求AC的值,进而利用三角形面积公式即可计算得解.
解答 (本题满分为12分) 解:(Ⅰ)在△ABD中,由,BD=$\frac{ABsin∠BAD}{sin∠ADB}$=$\frac{3\sqrt{6}sin\frac{7π}{12}}{sin\frac{π}{3}}$,
解:(Ⅰ)在△ABD中,由,BD=$\frac{ABsin∠BAD}{sin∠ADB}$=$\frac{3\sqrt{6}sin\frac{7π}{12}}{sin\frac{π}{3}}$,
∴BD=3$\sqrt{3}+3$. …(4分)
(Ⅱ)AD=$\frac{ABsinB}{sin∠ADB}$=$\frac{3\sqrt{6}sin\frac{π}{4}}{sin\frac{π}{3}}$,
∴AD=6,
在△ACD中,由余弦定理得:AC=$\sqrt{A{D}^{2}+C{D}^{2}-2AD•CD•cos∠ADC}$=14. …(8分)
∴S△ACD=$\frac{1}{2}$AD•DC•sin∠ADC=$\frac{1}{2}×6×10×\frac{\sqrt{3}}{2}$=15$\sqrt{3}$. …(12分)
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数且图象关于点$({\frac{π}{2},0})$对称 | B. | 偶函数且图象关于点(π,0)对称 | ||
| C. | 奇函数且图象关于直线$x=\frac{π}{2}$对称 | D. | 偶函数且图象关于点$({\frac{π}{2},0})$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
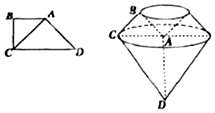 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
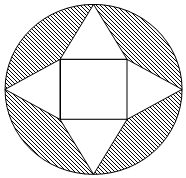 如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.| A. | $\frac{4\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{17}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com