

分析 证明DE∥AC,利用平行线的性质,可得$\frac{DB}{AB}$=$\frac{DE}{AC}$=$\frac{2}{3}$,设AD=x,则AB=3x,由射影定理可得AD,BD,再由射影定理可得CD.
解答 解:∵AC⊥BC,DE⊥BC,
∴DE∥AC,
∵AC=6,DE=4,
∴$\frac{DB}{AB}$=$\frac{DE}{AC}$=$\frac{2}{3}$,
设AD=x,则AB=3x,由射影定理可得36=x•3x,
∴x=2$\sqrt{3}$,
∴BD=4$\sqrt{3}$
由射影定理可得CD=$\sqrt{AD•DB}$=2$\sqrt{6}$.
故答案为:2$\sqrt{6}$.
点评 本题考查射影定理,考查平行线的性质的运用,属于基础题.


科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 时间代号x | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y (千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
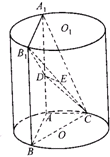 如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,且AB=AC=$\frac{1}{2}$AA1=2.
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,且AB=AC=$\frac{1}{2}$AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,3\sqrt{5})$ | B. | $[-\sqrt{5},\sqrt{5}]$ | C. | $(-3\sqrt{5},3\sqrt{5})$ | D. | $(0,\sqrt{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果a>b,那么ac2>bc2 | B. | 如果a>b,那么a2>b2 | ||
| C. | 如果a>b,ab>0,那么$\frac{1}{a}<\frac{1}{b}$ | D. | 如果x≠0,那么$x+\frac{1}{x}≥2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com