
| A. | $3\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | 3 |
分析 根据题意,由双曲线的方程可得a、b、c的值,即可得|F1F2|的值,由余弦定理可得|PF1||PF2|的值,进而有三角形面积公式计算可得答案.
解答 解:根据题意,双曲线方程为$\frac{x^2}{4}-\frac{y^2}{3}=1$,其中a=$\sqrt{4}$=2,b=$\sqrt{3}$,
则c=$\sqrt{3+4}$=$\sqrt{7}$,
则|F1F2|=2c=2$\sqrt{7}$,
由余弦定理可得:|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos60°,
又由||PF1|-|PF2||=2a=4,
则有|F1F2|2=(|PF1|-|PF2|)2+2|PF1||PF2|-2|PF1||PF2|cos60°,
即28=16+|PF1||PF2|,
解可得|PF1||PF2|=12,
S=$\frac{1}{2}$|PF1||PF2|sin60°=3$\sqrt{3}$;
故选:A.
点评 本题考查双曲线的几何性质,涉及余弦定理的应用,关键是求出|PF1||PF2|的值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
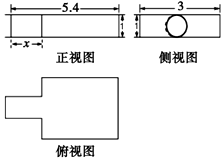 我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )
我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )| A. | 0.4π+11.4立方寸 | B. | 13.8立方寸 | C. | 12.6立方寸 | D. | 16.2立方寸 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
| 支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
| 年龄低于35岁 | 年龄不低于35岁 | 合计 | |
| 支持 | |||
| 不支持 | |||
| 合计 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com