
【题目】以椭圆![]() :
:![]() 的中心
的中心![]() 为圆心,
为圆心,![]() 为半径的圆称为该椭圆的“准圆”.设椭圆
为半径的圆称为该椭圆的“准圆”.设椭圆![]() 的左顶点为
的左顶点为![]() ,左焦点为
,左焦点为![]() ,上顶点为
,上顶点为![]() ,且满足
,且满足![]() ,
,![]() .
.
(1)求椭圆![]() 及其“准圆”的方程;
及其“准圆”的方程;
(2)若椭圆![]() 的“准圆”的一条弦
的“准圆”的一条弦![]() (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆![]() 交于
交于![]() 、
、![]() 两点,试证明:当
两点,试证明:当![]() 时,试问弦
时,试问弦![]() 的长是否为定值,若是,求出该定值;若不是,请说明理由.
的长是否为定值,若是,求出该定值;若不是,请说明理由.
【答案】(1)椭圆![]() 的方程为
的方程为![]() ;椭圆
;椭圆![]() 的“准圆”方程为
的“准圆”方程为![]() ;(2)弦
;(2)弦![]() 的长为定值
的长为定值![]() .
.
【解析】
试题分析:(1)求方程,关键是求![]() ,只要把两个已知条件转化为
,只要把两个已知条件转化为![]() 的方程即可,由
的方程即可,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,联立后可得结论;(2)这是定值问题,解题时设直线
,联立后可得结论;(2)这是定值问题,解题时设直线![]() 的方程为
的方程为![]() ,且与椭圆
,且与椭圆![]() 的交点
的交点![]() ,把直线方程与椭圆方程联立并消元后得关于
,把直线方程与椭圆方程联立并消元后得关于![]() 的一元二次方程,可得
的一元二次方程,可得![]() ,计算
,计算![]() ,由
,由![]() =0,可得
=0,可得![]() 的关系式,问题是弦长为定值,由于弦是定圆中的弦,因此只要求得圆心到直线的距离
的关系式,问题是弦长为定值,由于弦是定圆中的弦,因此只要求得圆心到直线的距离![]() ,如果
,如果![]() 为定值,则弦长也为定值.
为定值,则弦长也为定值.
试题解析:(1)设椭圆![]() 的左焦点
的左焦点![]()
![]() ,由
,由![]() 得
得![]() ,又
,又![]() ,即
,即![]() 且
且![]() ,所以
,所以![]() ,
,
则椭圆![]() 的方程为
的方程为![]() ;椭圆
;椭圆![]() 的“准圆”方程为
的“准圆”方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,且与椭圆
,且与椭圆![]() 的交点
的交点![]() ,
,
联列方程组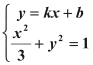 代入消元得:
代入消元得:![]()
由![]()
可得![]() 由
由![]() 得
得![]() 即
即![]()
![]() ,所以
,所以![]()
此时![]() 成立,
成立,
则原点![]() 到弦
到弦![]() 的距离
的距离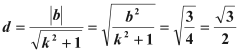 ,
,
得原点![]() 到弦
到弦![]() 的距离为
的距离为![]() ,则
,则![]() ,
,
故弦![]() 的长为定值.
的长为定值.


科目:高中数学 来源: 题型:
【题目】若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为y=2x2-3,值域为{1,5}的“孪生函数”共有( )
A.10个
B.9个
C.8个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155![]() 和195
和195![]() 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.

(1)求第七组的频率;
(2)估计该校的800名男生的身高的众数以及身高在180![]() 以上(含180
以上(含180![]() )的人数;
)的人数;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为![]() ,事件
,事件![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】编号1~15的小球共15个,求总体号码的平均值,试验者从中抽3个小球,以它们的平均数估计总体平均数,以编号2为起点,用系统抽样法抽3个小球,则这3个球的编号平均数是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区提倡低碳生活,环保出行,在小区提供自行车出租.该小区有40辆自行车供小区住户租赁使用,管理这些自行车的费用是每日92元,根据经验,若每辆自行车的日租金不超过5元,则自行车可以全部出租,若超过5元,则每超过1元,租不出的自行车就增加2辆,为了便于结算,每辆自行车的日租金![]() 元只取整数,用
元只取整数,用![]() 元表示出租自行车的日纯收入(日纯收入=一日出租自行车的总收入-管理费用)
元表示出租自行车的日纯收入(日纯收入=一日出租自行车的总收入-管理费用)
(1)求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)当租金定为多少时,才能使一天的纯收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.

(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]() ,某公司每年最多生产80台某种型号的大型计算机系统,生产
,某公司每年最多生产80台某种型号的大型计算机系统,生产![]() 台(
台(![]() )的收入函数为
)的收入函数为![]() (单位:万元),其成本函数为
(单位:万元),其成本函数为![]() (单位:万元),利润是收入与成本之差.
(单位:万元),利润是收入与成本之差.
(1)求利润函数![]() 及边际利润函数
及边际利润函数![]() ;
;
(2)①该公司生产多少台时获得的利润最大?
②利润函数![]() 与边际利润函数
与边际利润函数![]() 是否具有相同的最大值?
是否具有相同的最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若原命题为:“若a2+b2=0,则a、b全为0”,那么以下给出的4个结论:
①其逆命题为:若a、b全为0,则a2+b2=0;
②其否命题为:若a2+b2≠0,则a、b全不为0;
③其逆否命题为:若a、b全不为0,则a2+b2≠0;
④其否定为:若a2+b2=0,则a、b全不为0.
其中正确的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com