
 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则M的坐标________.
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则M的坐标________.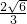 ,-1)
,-1) ,右准线方程:x=4.作出椭圆的右准线l,过M点作MN⊥l于N,根据圆锥曲线的统一定义,得
,右准线方程:x=4.作出椭圆的右准线l,过M点作MN⊥l于N,根据圆锥曲线的统一定义,得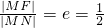 ,所以2|MF|=|MN|,欲求|MP|+2|MF|的最小值,即求|MP|+|MN|的最小值.作PN0⊥l于N0,交椭圆于M0,由平几知识可得,当动点M在椭圆上运动,与点M0重合时,|MP|+|MN|取到最小值.最后设出点M0的坐标,代入椭圆方程,解之即可得到使|MP|+2|MF|的值最小的点M的坐标.
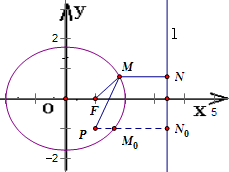
,所以2|MF|=|MN|,欲求|MP|+2|MF|的最小值,即求|MP|+|MN|的最小值.作PN0⊥l于N0,交椭圆于M0,由平几知识可得,当动点M在椭圆上运动,与点M0重合时,|MP|+|MN|取到最小值.最后设出点M0的坐标,代入椭圆方程,解之即可得到使|MP|+2|MF|的值最小的点M的坐标. ,
,
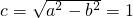
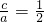 ,右准线方程:x=
,右准线方程:x=
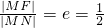 ,
,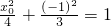 ,解之得x0=
,解之得x0= (舍负)
(舍负) ,-1).
,-1). ,-1).
,-1).

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源:2012年苏教版高中数学选修1-1 2.2椭圆练习卷(解析版) 题型:选择题
在椭圆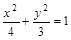 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( )
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( )
A. B.
B. C.3 D.4
C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学选修1-1 2.1椭圆练习卷(解析版) 题型:选择题
在椭圆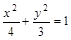 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( )
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则这一最小值是 ( )
A.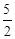 B.
B.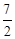 C.3 D.4
C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省南昌市四校高二(上)第二次联考数学试卷(理科)(解析版) 题型:填空题
 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则M的坐标 .
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使|MP|+2|MF|的值最小,则M的坐标 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com