
【题目】如图,已知四边形ABCD由Rt△ABC和Rt△BCD拼接而成,其中∠BAC=∠BCD=90°,∠DBC=30°,AB=AC,![]() ,将△ABC沿着BC折起,
,将△ABC沿着BC折起,
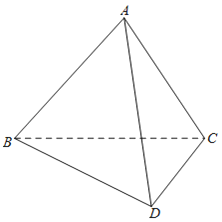
(1)若![]() ,求异面直线AB和CD所成角的余弦值;
,求异面直线AB和CD所成角的余弦值;
(2)当四面体ABCD的体积最大时,求二面角A﹣BC﹣D的余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据异面直角所成角的空间向量计算公式,再利用题给信息构造空间直角坐标系,即可求出所求角;
(2)当平面ABC⊥平面BCD时,四面体ABCD体积有最大值,即可得答案.
(1)因为∠BAC=90°,且AB=AC,BC![]() ,
,
∴![]() ,∴AB=AC=AD,
,∴AB=AC=AD,
∴作AO⊥平面BCD,垂足O必为△BCD的外心,
又因为△BCD中,∠BCD=90°,△BCD的外心在斜边中点处,即O点为BD中点,
则以OA方向建立z轴,过O点作x轴平行于BC,作y轴平行于CD,如图所示
得坐标,![]() ,
,![]() ,
,
∴![]()
∴![]() (0,﹣2,0),
(0,﹣2,0),![]() ,
,
设AB与CD所成角为![]() ,
,
则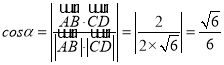 ;
;
(2)当平面ABC⊥平面BCD时,四面体ABCD体积有最大值,此时二面角A﹣BC﹣D为90°,其余弦值为0.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知动点P到两定点M(﹣3,0),N(3,0)的距离满足|PM|=2|PN|.
(1)求证:点P的轨迹为圆;
(2)记(1)中轨迹为⊙C,过定点(0,1)的直线l与⊙C交于A,B两点,求△ABC面积的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲船在岛A的正南B处,以![]() 的速度向正北航行,
的速度向正北航行,![]() ,同时乙船自岛A出发以
,同时乙船自岛A出发以![]() 的速度向北偏东60°的方向驶去,当甲、乙两船相距最近时,它们所航行的时间为( )
的速度向北偏东60°的方向驶去,当甲、乙两船相距最近时,它们所航行的时间为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的中心在坐标原点O,两个焦点分别为A(﹣1,0),B(1,0),一个顶点为H(2,0).
(1)求椭圆E的标准方程;
(2)对于x轴上的点P(t,0),椭圆E上存在点M,使得MP⊥MH,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ADC=60°,AD=AC=2,O为AC的中点,PO⊥平面ABCD且PO=4,M为PD的中点.
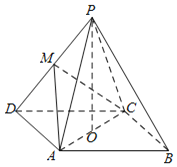
(1)证明:MO∥平面PAB;
(2)求直线AM与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别是( )
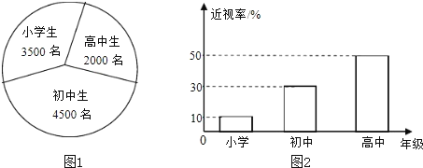
A.100,10B.100,20C.200,10D.200,20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用系统抽样法从140名学生中抽取容量为20的样本,将140名学生从1~140编号.按编号顺序平均分成20组(1~7号,8~14号,…,134~140号),若第17组抽出的号码为117,则第一组中按此抽样方法确定的号码是( )
A.7B.5C.4D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定的正整数k,若数列{an}满足![]()
=2kan对任意正整数n(n> k) 总成立,则称数列{an} 是“P(k)数列”.
(1)证明:等差数列{an}是“P(3)数列”;
若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com