
����Ŀ��ij����2010����2016��ũ������ͥ�˾�������y(��λ:ǧԪ)���������±�:
�ꡡ�� | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
��ݴ���t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�˾�������y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)��y����t�Ļع�ֱ�߷���;
(2)����(1)�еĻع鷽��,����2010����2016��õ���ũ������ͥ�˾�������ı仯���,��Ԥ��õ���2018��ũ������ͥ�˾�������.
��:�ع�ֱ�ߵ�б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�
���𰸡���1��![]() ����2��6.8ǧԪ
����2��6.8ǧԪ
����������������1��������������������ûع鷽�̼��ɣ�
��2����ϻع鷽�̵�Ԥ�����úͣ�1���еĽ����������㼴��������ս��.
�����(1)���������ݼ����
![]() ��
��
![]() ��
��
![]() ��
��
![]()
=(-3)��(-1.4)+(-2)��(-1)+(-1)��(-0.7)+0��0.1+1��0.5+2��0.9+3��1.6=14,
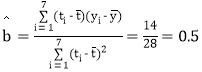 ��
��
![]() ��
��
����ع鷽��![]()
(2)��(1)![]() 2010����2016��õ���ũ������ͥ�˾���������������,ƽ��ÿ������0.5ǧԪ.
2010����2016��õ���ũ������ͥ�˾���������������,ƽ��ÿ������0.5ǧԪ.
��2018�����ݴ���t=9����(1)�еĻع鷽��,![]()
��Ԥ��õ���2018��ũ������ͥ�˾�������Ϊ6.8ǧԪ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���֪����f��x��=![]()
��1���жϺ���������[1,+�����ϵĵ�����,���ö���֤����Ľ��ۣ�
��2����ú���������[1,4]�ϵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x1 �� x2����xn����ƽ����Ϊx��������y1 �� y2 �� ����ym����ƽ����Ϊ ![]() ��
�� ![]() ��
�� ![]() ������������x1 �� x2����xn �� y1 �� y2 �� ����ym����ƽ����
������������x1 �� x2����xn �� y1 �� y2 �� ����ym����ƽ���� ![]() =��
=�� ![]() +��1������
+��1������ ![]() ������0������
������0������ ![]() ����n��m�Ĵ�С��ϵΪ�� ��
����n��m�Ĵ�С��ϵΪ�� ��
A.n��m
B.n��m
C.n=m
D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����O��0��0����A����2��1����B��2��1��������C������һ��M��x��y������| ![]() +
+ ![]() |=
|= ![]() ��
�� ![]() +
+ ![]() ��+2��
��+2��
��1��������C�ķ��̣�
��2������Q��x0 �� y0������2��x0��2��������C�ϣ�����C�ڵ�Q��������Ϊֱ��l���Ƿ���ڶ���P��0��t����t��0����ʹ��l��PA��PB���ཻ������ֱ�ΪD��E���ҡ�QAB���PDE�����֮���dz����������ڣ���t��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��I����![]() ��
��![]() �ļ�ֵ�㣮��ʵ��
�ļ�ֵ�㣮��ʵ��![]() ��ֵ��������
��ֵ��������![]() �ĵ������䣻
�ĵ������䣻
��II��֤������![]() ʱ��
ʱ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һλͬѧ���↑��һ��С����,��Ϊ���о����¶��Ȳ����۵�Ӱ��,����ͳ��,�õ�һ�������Ȳ豭���뵱�����µĶԱȱ�����:
����x/�� | -5 | 0 | 4 | 7 | 12 | 15 | 19 | 23 | 27 | 31 | 36 |
�Ȳ����۱���y/�� | 156 | 150 | 132 | 128 | 130 | 116 | 104 | 89 | 93 | 76 | 54 |
(1)����ɢ��ͼ;
(2)���ܴ�ɢ��ͼ�з����������Ȳ�����۱���֮���ϵ��һ�������?
(3)������Ƴ����Թ�ϵ�Ļ�,�뻭��һ��ֱ�������Ƶر�ʾ�������Թ�ϵ;
(4)������ع�ֱ�߷���;
(5)����(4)�Ļع鷽��,��ij���������2 ��,Ԥ����һ�������Ȳ�ı���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���Բ ![]() ��a��b��0�������ҽ���ֱ�ΪF1����c��0����F2��c��0������֪��1��e���ͣ�e��
��a��b��0�������ҽ���ֱ�ΪF1����c��0����F2��c��0������֪��1��e���ͣ�e�� ![]() ��������Բ�ϣ�����eΪ��Բ�������ʣ�
��������Բ�ϣ�����eΪ��Բ�������ʣ� 
��1������Բ�ķ��̣�
��2����A��B����Բ��λ��x���Ϸ������㣬��ֱ��AF1��ֱ��BF2ƽ�У�AF2��BF1���ڵ�P��
��i����AF1��BF2= ![]() ����ֱ��AF1��б�ʣ�
����ֱ��AF1��б�ʣ�
��ii����֤��PF1+PF2�Ƕ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �У���
�У���![]() ���ı���
���ı���![]() �����ģ�����ֱ��
�����ģ�����ֱ��![]() ������˵����ȷ���ǣ� ��
������˵����ȷ���ǣ� ��
A. ![]() B.
B. ![]()
C. ![]() ƽ��
ƽ��![]() D.
D. ![]() ƽ��
ƽ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ֱ������ϵ![]() �У�Բ
�У�Բ![]() ����ͨ����Ϊ
����ͨ����Ϊ![]() . ��������ԭ��Ϊ���㣬
. ��������ԭ��Ϊ���㣬![]() ��������Ϊ����ļ�����ϵ�У�ֱ��
��������Ϊ����ļ�����ϵ�У�ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
���� д��Բ ![]() �IJ������̺�ֱ��
�IJ������̺�ֱ��![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
�� �� �� ��ֱ��![]() ��
��![]() ���
���![]() ��Ľ���ֱ�Ϊ
��Ľ���ֱ�Ϊ![]() ��
��![]() ΪԲ
ΪԲ![]() �ϵ�����һ�㣬��
�ϵ�����һ�㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���𰸡�(1)![]() ;
;![]() .
.
(2)![]() .
.
�������������������(I)����Բ�ĺͰ뾶,д��Բ�IJ�������,��Բ�ļ����귽��չ�����ֱ�����귽��.(II)���![]() ���������, ���
���������, ���![]() ����������
����������![]() ,�������Ǻ�����ֵ�������ȡֵ��Χ.
,�������Ǻ�����ֵ�������ȡֵ��Χ.
�����������
����Բ![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������.
������.
ֱ��![]() ��ֱ�����귽��Ϊ
��ֱ�����귽��Ϊ![]() .
.
������ֱ��![]() �ķ���
�ķ���![]() �ɵõ�
�ɵõ�![]() ����
����![]() .
.
���![]() ����
����![]()
![]() .
.
![]()
![]() .
.
�ɣ���֪![]() ����
����![]()
![]()
![]() .
.
��Ϊ![]() ������
������![]() .
.
�����͡������
��������
23
����Ŀ��ѡ��4-5������ʽѡ��
��֪����![]() ��
�� ![]() .
.
��������������![]() ��
�� ![]() ������
������![]() ����
����![]() ��ֵ��
��ֵ��
����������![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com