
已知函数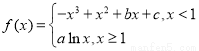 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点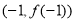 处的切线斜率为
处的切线斜率为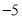 .
.
(1) 求实数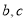 的值;
的值;
(2) 求函数 在区间
在区间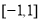 上的最小值;
上的最小值;
(3) 若函数 的图像上存在两点
的图像上存在两点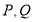 ,使得对于任意给定的正实数
,使得对于任意给定的正实数 都满足
都满足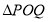 是以
是以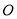 为直角顶点的直角三角形,且三角形斜边中点在
为直角顶点的直角三角形,且三角形斜边中点在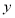 轴上,求点
轴上,求点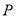 的横坐标的取值范围.
的横坐标的取值范围.
(1)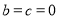 ;(2)
;(2)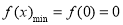 ;(3)
;(3)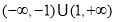 .
.
【解析】
试题分析:(1)根据图像过原点得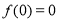 ,又切线斜率等于切点处导数值,得
,又切线斜率等于切点处导数值,得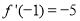 ,解出
,解出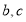 ;(2)
;(2)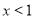 时
时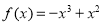 ,对
,对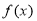 求导以判断函数
求导以判断函数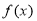 的单调性,得
的单调性,得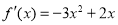 ,
,
令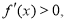 则
则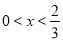 ,令
,令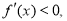 则
则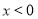 或
或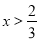 ,
,
故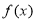 在
在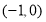 单调递减,在
单调递减,在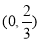 单调递增,在
单调递增,在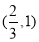 单调递减,
单调递减,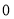 为极小值点,
为极小值点,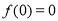 ,
,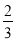 为极大值点,
为极大值点,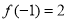 ,
,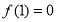 ,
,
比较极小值与区间端点处函数值,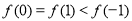 ,得
,得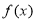 在
在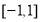 上的最小值为0,当
上的最小值为0,当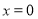 或1时取得;(3)设
或1时取得;(3)设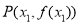 ,利用
,利用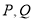 横坐标的对称关系得出
横坐标的对称关系得出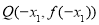 ,由
,由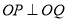 得
得 ,于是
,于是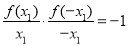 ①,然后对
①,然后对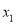 以
以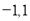 为分界点分类讨论方程①是否存在解,当
为分界点分类讨论方程①是否存在解,当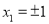 时,都有
时,都有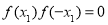 ,故方程①无解;当
,故方程①无解;当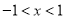 时,
时,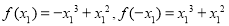 ,代入①化简得
,代入①化简得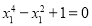 ,该方程判别式小于0,故方程无解;当
,该方程判别式小于0,故方程无解;当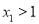 时,
时,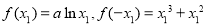 代人①化简得
代人①化简得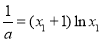 ,再考虑此方程是否有解,令
,再考虑此方程是否有解,令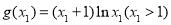 ,求导分析知
,求导分析知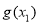 是增函数,注意到
是增函数,注意到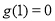 ,故
,故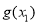 的值域是
的值域是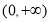 ,因此方程①对任意正实数
,因此方程①对任意正实数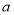 恒有解;当
恒有解;当 时,由
时,由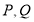 横坐标的对称性同理可得,方程①对任意正实数
横坐标的对称性同理可得,方程①对任意正实数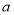 恒有解,综上可得点
恒有解,综上可得点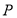 的横坐标的取值范围.
的横坐标的取值范围.
试题解析:(1)当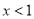 时,
时,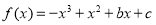 ,
,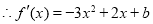 ,
,
依题意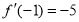 ,
,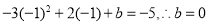 ,
,
又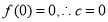 ,故
,故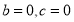 ;...............3分
;...............3分
(2)当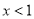 时,
时,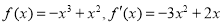 ,
,
令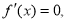 有
有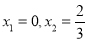 ,故
,故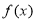 在
在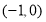 单调递减;在
单调递减;在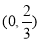 单调递增;
单调递增;
在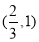 单调递减.又
单调递减.又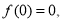
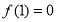 ,
,
所以当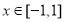 时,
时,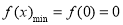 ; 6分
; 6分
(3)设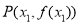 ,因为
,因为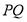 中点在
中点在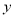 轴上,所以
轴上,所以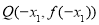 ,
,
又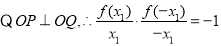 ①,
①,
(ⅰ)当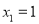 时,
时,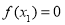 ,当
,当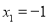 时,
时, .故①不成立 7分
.故①不成立 7分
(ⅱ)当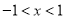 时,
时,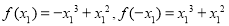 代人①得:
代人①得:
 ,
,
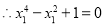 无解; 8分
无解; 8分
(ⅲ)当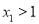 时,
时,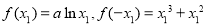 代人①得:
代人①得:
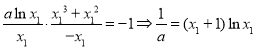 ②,
②,
设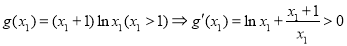 ,则
,则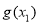 是增函数.
是增函数.
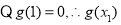 的值域是
的值域是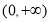 . 10分
. 10分
所以对于任意给定的正实数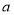 ,②恒有解,故满足条件.
,②恒有解,故满足条件.
(ⅳ)由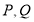 横坐标的对称性同理可得,当
横坐标的对称性同理可得,当 时,
时,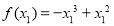
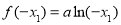 ,代人①得:
,代人①得:
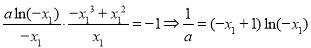 ③
③
设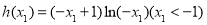 ,令
,令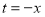 ,则
,则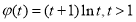
由上面知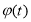 的值域是
的值域是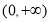
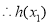 的值域为
的值域为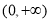 .
.
所以对于任意给定的正实数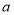 ,③恒有解,故满足条件. 12分
,③恒有解,故满足条件. 12分
综上所述,满足条件的点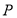 的横坐标的取值范围为
的横坐标的取值范围为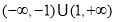 ..........14分
..........14分
考点:1、导数与切线关系;2、函数单调性与最值;3、分类讨论的思想;4、函数与方程的思想.


科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考理科数学试卷(解析版) 题型:选择题
已知双曲线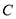 :
: (
(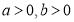 )的离心率为
)的离心率为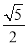 ,则
,则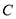 的渐近线方程为( )
的渐近线方程为( )
A. B.
B. C.
C.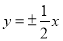 D.
D.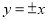
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试理科数学试卷(解析版) 题型:选择题
已知实数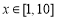 ,执行如图所示的程序框图,则输出x的值不小于55的概率为( )
,执行如图所示的程序框图,则输出x的值不小于55的概率为( )
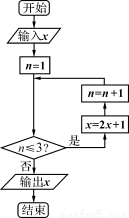
(A)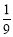 (B)
(B)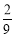 (C)
(C)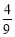 (D)
(D)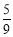
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试文科数学试卷(解析版) 题型:选择题
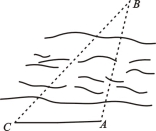
如图,已知A,B两点分别在河的两岸,某测量者在点A所在的河岸边另选定一点C,测得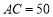 m,
m,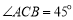 ,
,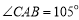 ,则A、B两点的距离为( )
,则A、B两点的距离为( )
(A)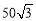 m (B)
m (B)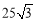 m (C)
m (C)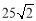 m (D)
m (D) m
m
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三第六期3月阶段性考试文科数学试卷(解析版) 题型:选择题
已知函数 (
( ),则( )
),则( )
A. 必是偶函数 B.当
必是偶函数 B.当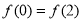 时,
时, 的图象必须关于
的图象必须关于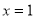 直线对称;
直线对称;
C. 有最大值
有最大值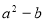 D. 若
D. 若 ,则
,则 在区间
在区间 上是增函数;
上是增函数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com