
【题目】已知函数![]() 存在唯一的极值点
存在唯一的极值点![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)求导得到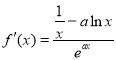 ,设
,设![]() ,讨论
,讨论![]() ,
,![]() ,
,![]() ,
,![]() 四种情况,根据零点存在定理计算得到答案.
四种情况,根据零点存在定理计算得到答案.
(2)根据题意得到![]() ,
,![]() ,根据
,根据![]() 得到
得到![]() ,化简得到答案.
,化简得到答案.
(1)函数的定义域为![]() ,
,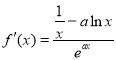 ,令
,令![]() ,
,
①若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递增,不合题意;
上单调递增,不合题意;
②若![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
(ⅰ)若![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,不合题意;
上单调递增,不合题意;
(ⅱ)若![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,
,
因为![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上有两个变号零点,所以
上有两个变号零点,所以![]() 有两个极值点,不合题意;
有两个极值点,不合题意;
③若![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
且![]() ,
,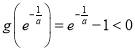 ,存在唯一
,存在唯一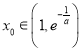 ,使
,使![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 是
是![]() 的唯一极值点,符合题意;
的唯一极值点,符合题意;
综上,![]() 的取值范围是
的取值范围是![]() .
.
(2)由(1)可知,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
由(1)可知函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
现证明不等式:![]() ,其中
,其中![]()
要证![]() ,即证
,即证![]() ,即证
,即证![]() ,
,
即证![]() ,易知成立.
,易知成立.
所以![]() ,即
,即![]() ,
,
即![]() ,所以
,所以![]() ,证毕.
,证毕.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() (其中
(其中![]() ,点P的轨迹记为曲线
,点P的轨迹记为曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线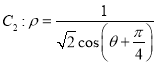 上.
上.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() ,
,![]() 时,求曲线
时,求曲线![]() 与曲线
与曲线![]() 的公共点的极坐标
的公共点的极坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
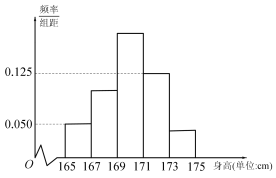
【题目】国庆70周年阅兵式上的女兵们是一道靓丽的风景线,每一名女兵都是经过层层筛选才最终入选受阅方队,筛选标准非常严格,例如要求女兵身高(单位:cm)在区间![]() 内.现从全体受阅女兵中随机抽取200人,对她们的身高进行统计,将所得数据分为
内.现从全体受阅女兵中随机抽取200人,对她们的身高进行统计,将所得数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,得到如图所示的频率分布直方图,其中第三组的频数为75,最后三组的频率之和为0.7.
五组,得到如图所示的频率分布直方图,其中第三组的频数为75,最后三组的频率之和为0.7.
(1)请根据频率分布直方图估计样本的平均数![]() 和方差
和方差![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)根据样本数据,可认为受阅女兵的身高X(cm)近似服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)求![]() ;
;
(ii)若从全体受阅女兵中随机抽取10人,求这10人中至少有1人的身高在174.28cm以上的概率.
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过
,过![]() 的直线与抛物线
的直线与抛物线![]() 相交于
相交于![]() 两点.
两点.
(1)若点![]() 是点
是点![]() 关于坐标原点
关于坐标原点![]() 的对称点,求
的对称点,求![]() 面积的最小值;
面积的最小值;
(2)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出![]() 的方程和定值;若不存在,说明理由.
的方程和定值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十项全能是由跑、跳、投等10个田径项目组成的综合性男子比赛项目,按照国际田径联合会制定的田径运动全能评分表计分,然后将各个单项的得分相加,总分多者为优胜.下面是某次全能比赛中甲、乙两名运动员的各个单项得分的雷达图.
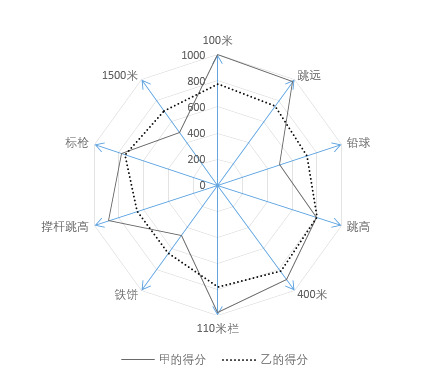
下列说法错误的是( )
A.在100米项目中,甲的得分比乙高
B.在跳高和标枪项目中,甲、乙的得分基本相同
C.甲的各项得分比乙更均衡
D.甲的总分高于乙的总分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】红铃虫(Pectinophora gossypiella)是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型①![]() ,②
,②![]() 分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
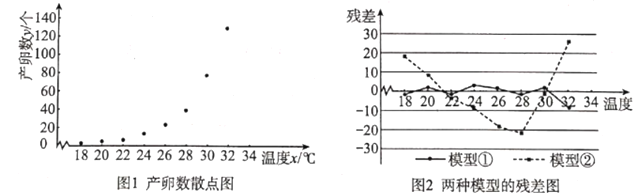
根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
|
25 | 2.89 | 646 | 168 | 422688 | 48.48 | 70308 |
表中![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(2)根据(1)中所选择的模型,求出y关于x的回归方程(系数精确到0.01),并求温度为34℃时,产卵数y的预报值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为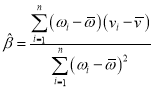 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为菱形,
的底面为菱形,![]() ,
,![]() .平面
.平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() //平面
//平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒.
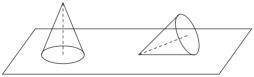
(1)求该圆锥的表面积![]() 和体积
和体积![]() ;
;
(2)求该圆锥被吹倒后,其最高点到桌面的距离![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com