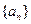
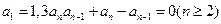
(1)求数列
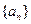
的通项;
(2)若
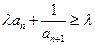
对任意
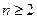
的整数恒成立,求实数
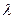
的取值范围;
(3)设数列
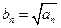
,
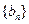
的前
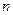
项和为
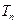
,求证:
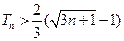
(1)
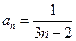
(2)
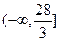
(1)将
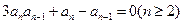
整理得:
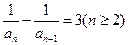
………1分
所以
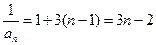
,即
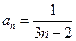
………………3分
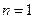
时,上式也成立,所以,
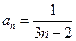
………………5分
(2)若
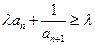
恒成立,即
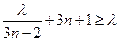
恒成立 ………………6分
整理得:
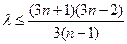
令
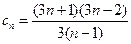
………7分
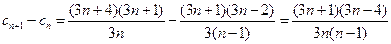
……………8分
因为
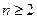
,所以上式

,即
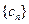
为单调递增数列,所以
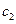
最小,
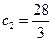
,
所以
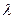
的取值范围为
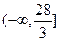
……………………10分
(3)由
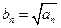
,得
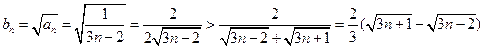
所以,
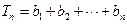
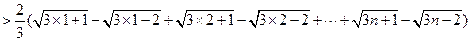
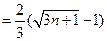
……………………14分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
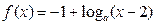
(
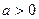
,且
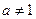
),
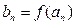
,
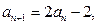
且
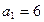
,
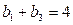
(1)证明:
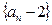
为等比数列
(2)求
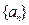
和
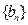
的通项公式。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设
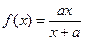
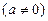
,令
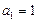
,
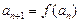
,又
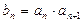
,
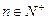
.
(Ⅰ)判断数列
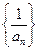
是等差数列还是等比数列并证明;
(Ⅱ)求数列
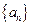
的通项公式;
(Ⅲ)求数列
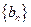
的前

项和.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列
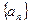
的各项均为正数,它的前n项和S
n满足
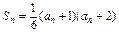
,并且
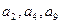
成等比数列.
(I)求数列
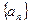
的通项公式;
(II)设
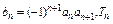
为数列
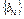
的前n项和,求
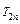
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
数列{
an}的前
n项和记为
Sn,
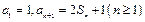
(1)求{
an}的通项公式;
(2)等差数列{
bn}的各项为正,其前
n项和为
Tn,且
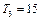
,又
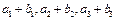
成等比数列,求
Tn
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
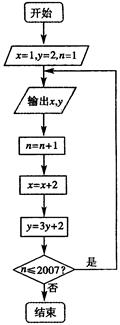
根据如图所示的程序框图,将输出的
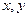
值依
次分别记为
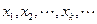
;
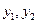
,…,
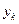
,….
(Ⅰ)分别求数列
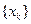
和
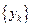
的通项公式;
(Ⅱ)令
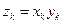
,求数列
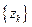
的前
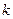
项和
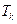
,
其中
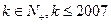
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题



⑴求数列

的通项公式;
⑵设

,若

对

恒成立,求实数

的取值范围;
⑶是否存在以

为首项,公比为

的数列

,

,使得数列

中每一项都是数列

中不同的项,若存在,求出所有满足条件的数列

的通项公式;若不存在,说明理由
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列
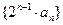
的前
n项和
Sn=9-6
n.
(1)求数列
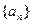
的通项公式.
(2)设
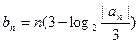
,求数列
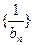
的前
n项和.
查看答案和解析>>

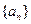
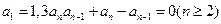
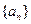 的通项;
的通项;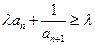 对任意
对任意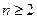 的整数恒成立,求实数
的整数恒成立,求实数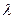 的取值范围;
的取值范围;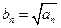 ,
,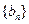 的前
的前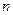 项和为
项和为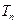 ,求证:
,求证: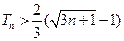



 的通项公式;
的通项公式; ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由