
【题目】中华民族是一个传统文化丰富多彩的民族,各民族有许多优良的传统习俗,如过大年吃饺子,元宵节吃汤圆,端午节吃粽子,中秋节吃月饼等等,让人们感受到浓浓的节目味道. 某小区有1200户家庭,全部居民在小区的8栋楼内,各家庭在过年时各自包有肉馅饺子、蛋馅饺子和素馅饺子三种味道的饺子(假设每个家庭包有且只包有这三种味道中的一种味道的饺子).
(1)现根据饺子的不同味道用分层抽样的方法从该小区随机抽样抽取![]() 户家庭,其中有10户家庭包的是素馅饺子,在抽取家庭中包肉馅饺子和蛋馅饺子的家庭分布在8栋楼内的住户数记录为如图所示的茎叶图,已知肉馅饺子数的中位数为10,蛋馅饺子数的平均数为5,求该小区包肉馅饺子的户数;
户家庭,其中有10户家庭包的是素馅饺子,在抽取家庭中包肉馅饺子和蛋馅饺子的家庭分布在8栋楼内的住户数记录为如图所示的茎叶图,已知肉馅饺子数的中位数为10,蛋馅饺子数的平均数为5,求该小区包肉馅饺子的户数;
(2)现从包肉馅饺子的家庭中随机抽取100个家庭调查包饺子的用肉量(单位: ![]() )得到了如图所示的频率分布直方图,若用肉量在第1小组
)得到了如图所示的频率分布直方图,若用肉量在第1小组![]() 内的户数为
内的户数为![]() (
(![]() 为茎叶图中的
为茎叶图中的![]() ),试估计该小区过年时各户用于包饺子的平均用肉量(各小组数据以组中值为代表).
),试估计该小区过年时各户用于包饺子的平均用肉量(各小组数据以组中值为代表).
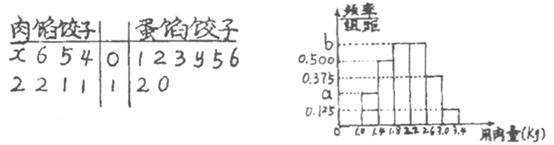
【答案】 (1)该小区包肉馅饺子的户数为700户.(2)估计该小区过年时各户用于包饺子的平均用量为2.12![]() .
.
【解析】试题分析:(1)根据中位数的定义,可知![]() ,再根据平均数的公式可解得
,再根据平均数的公式可解得![]() ,可知肉馅的有70户,蛋馅的有40户,素馅的有10户,公120户,那么根据分层抽样方法的计算公式,可知该小区包肉馅的户数,(2)根据(1)的结果可知第一组的频数为10,根据频率分布直方图的频率公式可求得
,可知肉馅的有70户,蛋馅的有40户,素馅的有10户,公120户,那么根据分层抽样方法的计算公式,可知该小区包肉馅的户数,(2)根据(1)的结果可知第一组的频数为10,根据频率分布直方图的频率公式可求得![]() ,再根据频率和为1求得
,再根据频率和为1求得![]() ,最后根据平均数公式:每一组小矩形的中点乘以该组的频率求和,即平均数.
,最后根据平均数公式:每一组小矩形的中点乘以该组的频率求和,即平均数.
试题解析:(1)依题意![]() ,
, ![]()
又![]() ,
, ![]() , n=70+40+10=120
, n=70+40+10=120
因为是分层抽样,
故该小区中包肉馅饺子的户数为![]()
即该小区包肉馅饺子的户数为700户.
(2)由(1)知![]()
![]() ,故第1小组的频数为10,频率为
,故第1小组的频数为10,频率为![]() .
.![]()
![]()
![]()
根据样本频率分布直方图可得100户家庭的平均用肉量约为
![]()
![]()
据此估计该小区过年时各户用于包饺子的平均用量为2.12![]() .
.


科目:高中数学 来源: 题型:
【题目】某商店计划每天购进某商品若干件,商店每销售一件该商品可获利润60元,若供大于求,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利40元.
(1)若商品一天购进该商品10件,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:件,
(单位:件,![]() )的函数解析式;
)的函数解析式;
(2)商店记录了50天该商品的日需求量![]() (单位:件,
(单位:件,![]() ),整理得下表:
),整理得下表:

若商店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求当天的利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下山至
处下山至![]() 处有两种路径,一种是从
处有两种路径,一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() .假设缆车匀速直线运动的速度为
.假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为
长为![]() ,经测量,
,经测量,![]() ,
,![]() .
.

(1)求索道![]() 的长;
的长;
(2)为使两位游客在![]() 处互相等待的时间不超过3分钟,乙步行的速度应该控制在什么范围内?
处互相等待的时间不超过3分钟,乙步行的速度应该控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 内有一点
内有一点![]() ,
,![]() 为圆
为圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线与
的垂直平分线与![]() 的连线交于点
的连线交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程.
的轨迹方程.
(Ⅱ)若动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 、
、![]() 两点,且以
两点,且以![]() 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点![]() .问是否存在一个定圆与动直线
.问是否存在一个定圆与动直线![]() 总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月16日下午5时左右,今年第22号台风“山竹”在广东江门川岛镇附近正面登陆,给当地人民造成了巨大的财产损失,某记者调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,并作出如下频率分布直方图.
五组,并作出如下频率分布直方图.
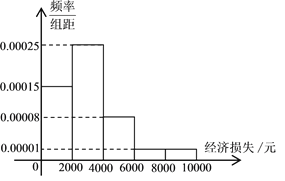
(Ⅰ)根据频率分布直方图估计该小区居民由于台风造成的经济损失的众数和平均值.
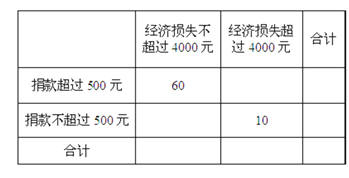
(Ⅱ)“一方有难,八方支援”,台风后居委会号召小区居民为台风重灾区捐款,![]() 记者调查的100户居民捐款情况如下表格,在如图表格空白处填写正确数字,并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
记者调查的100户居民捐款情况如下表格,在如图表格空白处填写正确数字,并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某葡萄基地的种植专家发现,葡萄每株的收获量![]() (单位:
(单位: ![]() )和与它“相近”葡萄的株数
)和与它“相近”葡萄的株数![]() 具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时,该葡萄每株收获量的相关数据如下:
),并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时,该葡萄每株收获量的相关数据如下:
| 1 | 2 | 3 | 5 | 6 | 7 |
| 15 | 13 | 12 | 10 | 9 | 7 |
(1)求该葡萄每株的收获量![]() 关于它“相近”葡萄的株数
关于它“相近”葡萄的株数![]() 的线性回归方程及
的线性回归方程及![]() 的方差
的方差![]() ;
;
(2)某葡萄专业种植户种植了1000株葡萄,每株“相近”的葡萄株数按2株计算,当年的葡萄价格按10元/ ![]() 投入市场,利用上述回归方程估算该专业户的经济收入为多少万元;(精确到0.01)
投入市场,利用上述回归方程估算该专业户的经济收入为多少万元;(精确到0.01)
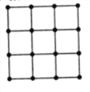
(3)该葡萄基地在如图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株葡萄,其中每个小正方形的面积都为![]() ,现在所种葡萄中随机选取一株,求它的收获量的分布列与数学期望.(注:每株收获量以线性回归方程计算所得数据四舍五入后取的整数为依据)
,现在所种葡萄中随机选取一株,求它的收获量的分布列与数学期望.(注:每株收获量以线性回归方程计算所得数据四舍五入后取的整数为依据)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com