
| A. | $\sqrt{5}$-1 | B. | 2$+\sqrt{5}$ | C. | 3$+\sqrt{5}$ | D. | 5$+\sqrt{5}$ |
分析 设P(m,$\frac{1}{8}$m2),分别过B、P作直线y=-2的垂线,垂足为D、E,由已知条件推导出|FC|=|BD|=2,设直线PQ的方程为y=kx+2,代入C:x2=8y得x2-8kx-16=00,由此能求出|PF|.
解答 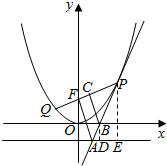 解:设P(m,$\frac{1}{8}$m2),分别过B、P作直线y=-2的垂线,垂足为D、E,
解:设P(m,$\frac{1}{8}$m2),分别过B、P作直线y=-2的垂线,垂足为D、E,
∵BC∥AF,∴$\frac{|FC|}{|FP|}$=$\frac{|AB|}{|AP|}$=$\frac{|BD|}{|PE|}$,
∵|FP|=|PE|,∴|FC|=|BD|=2,
设直线PQ的方程为y=kx+2,代入C:x2=8y得x2-8kx-16=0,
∴m•xQ=-16,∴xQ=-$\frac{16}{m}$,∴yQ=$\frac{32}{{m}^{2}}$,
∵|PF|=$\frac{1}{8}$m2+2,∴|PC|=$\frac{1}{8}$m2,
∵|QF|=$\frac{32}{{m}^{2}}$+2,|PC|=|QF|,
∴得$\frac{1}{8}$m2=$\frac{32}{{m}^{2}}$+2,
∴m4-16m2-256=0,解得m2=8+8$\sqrt{5}$
∴|PF|=$\frac{1}{8}$m2+2=3+$\sqrt{5}$.
故选:C.
点评 本题考查考查线段长的求法,考查函数与方程思想、等价转化思想的合理运用,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | $[\frac{3}{2},1+\sqrt{3}]$ | B. | $[2,1+\sqrt{3}]$ | C. | [1,3] | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
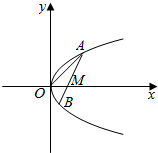 如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线C.
如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行 | B. | 重合 | C. | 相交 | D. | 垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
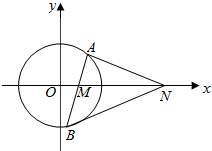 已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的上方
已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的上方查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com