
已知函数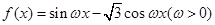 的图象与
的图象与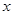 轴的两个相邻交点的距离等于
轴的两个相邻交点的距离等于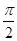 ,则为得到函数
,则为得到函数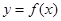 的图象可以把函数
的图象可以把函数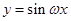 的图象上所有的点( )
的图象上所有的点( )
A.向右平移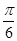 ,再将所得图象上所有的点的纵坐标变为原来的2倍 ,再将所得图象上所有的点的纵坐标变为原来的2倍 |
B.向右平移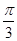 ,再将所得图象上所有的点的纵坐标变为原来的2倍 ,再将所得图象上所有的点的纵坐标变为原来的2倍 |
C.向左平移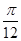 ,再将所得图象上所有的点的纵坐标变为原来的 ,再将所得图象上所有的点的纵坐标变为原来的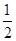 倍 倍 |
D.向左平移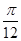 ,再将所得图象上所有的点的纵坐标变为原来的2倍 ,再将所得图象上所有的点的纵坐标变为原来的2倍 |
A
解析考点:由y=Asin(ωx+φ)的部分图象确定其解析式;函数y=Asin(ωx+φ)的图象变换.专题:计算题.
分析:先利用两角差的正弦公式将函数f(x)=sinωx- 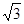 cosωx化为y=Asin(ωx+φ)的形式,再利用周期公式计算ω的值,最后由三角函数图象变换理论作出正确判断
cosωx化为y=Asin(ωx+φ)的形式,再利用周期公式计算ω的值,最后由三角函数图象变换理论作出正确判断
解答:解:∵f(x)=sinωx- 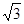 cosωx=2(
cosωx=2(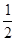 sinωx-
sinωx- 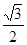 cosωx)=2sin(ωx-
cosωx)=2sin(ωx-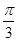 )
)
又∵f(x)的图象与x轴的两个相邻交点的距离等于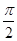 ,
,
∴函数f(x)的最小正周期为T=2×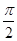 =π
=π
∴2π /ω =π,ω=2
∴f(x)=2sin(2x-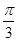 )=2sin2(x-
)=2sin2(x-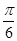 ),
),
∴为得到函数y=f(x)的图象可以把函数y=sin2x的图象上所有的点向右平移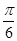 ,得y=sin2(x-
,得y=sin2(x-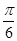 )的图象,再将所得图象上所有的点的纵坐标变为原来的2倍,得y=2sin2(x-
)的图象,再将所得图象上所有的点的纵坐标变为原来的2倍,得y=2sin2(x-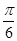 )的图象
)的图象
故选A.
点评:本题考查了三角变换公式的应用,三角函数的图象和性质,周期公式,三角函数图象变换的方法等基础知识


科目:高中数学 来源:2013届重庆市高三上学期期中考试文科数学试卷(解析版) 题型:解答题
已知函数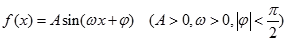 的图象与
的图象与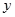 轴的交点为
轴的交点为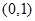 ,它在
,它在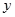 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为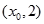 和
和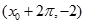 .
.
(Ⅰ)求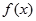 的解析式及
的解析式及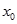 的值;
的值;
(Ⅱ)若锐角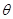 满足
满足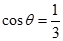 ,求
,求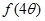 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年新疆乌鲁木齐一中高三第一次月考理科数学试卷 题型:解答题
(10分)已知函数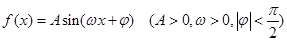 的图象与
的图象与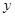 轴
轴
的交点为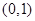 ,它在
,它在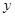 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为 和
和
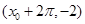 .
.
(1)求 的解析式及
的解析式及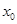 的值;
的值;

查看答案和解析>>
科目:高中数学 来源:2010-2011学年天津市高三十校联考理科数学 题型:选择题
已知函数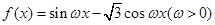 的图象与
的图象与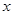 轴的两个相邻交点的距离等于
轴的两个相邻交点的距离等于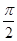 ,则为得到函数
,则为得到函数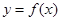 的图象可以把函数
的图象可以把函数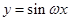 的图象上所有的点( )
的图象上所有的点( )
A. 向右平移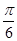 ,再将所得图象上所有的点的纵坐标变为原来的2倍
,再将所得图象上所有的点的纵坐标变为原来的2倍
B. 向右平移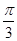 ,再将所得图象上所有的点的纵坐标变为原来的2倍
,再将所得图象上所有的点的纵坐标变为原来的2倍
C. 向左平移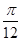 ,再将所得图象上所有的点的纵坐标变为原来的
,再将所得图象上所有的点的纵坐标变为原来的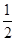 倍
倍
D. 向左平移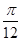 ,再将所得图象上所有的点的纵坐标变为原来的2倍
,再将所得图象上所有的点的纵坐标变为原来的2倍
查看答案和解析>>
科目:高中数学 来源:2013届辽宁省辽南协作体高一下学期期中考试数学(理) 题型:解答题
(本小题满分12分)
已知函数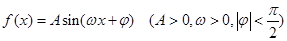 的图象与
的图象与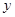 轴的交点为
轴的交点为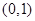 ,它在
,它在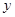 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为 和
和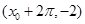 .
.
(1)求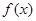 的解析式;
的解析式;
(2)若锐角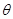 满足
满足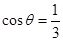 ,求
,求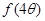 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013届山东省高一下学期期末考试数学 题型:解答题
(本小题满分12分)
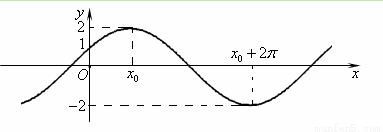
已知函数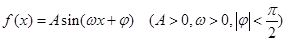 的图象与
的图象与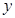 轴的交点为
轴的交点为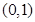 ,它在
,它在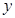 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为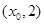 和
和 .
.
(1)求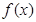 的解析式;
的解析式;
(2)若锐角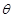 满足
满足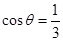 ,求
,求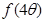 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com