
【题目】函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是( )
A.
B.
C.
D.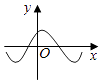
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】北京101中学校园内有一个“少年湖”,湖的两侧有一个音乐教室和一个图书馆,如图,若设音乐教室在A处,图书馆在B处,为测量A,B两地之间的距离,某同学选定了与A,B不共线的C处,构成△ABC,以下是测量的数据的不同方案:①测量∠A,AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B. 其中一定能唯一确定A,B两地之间的距离的所有方案的序号是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD的底面为等腰梯形, AB∥CD,AC⊥BD,垂足为H, PH是四棱锥的高,E为AD中点,设![]()
1)证明:PE⊥BC;
2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a∈Z,已知定义在R上的函数f(x)=2x4+3x3﹣3x2﹣6x+a在区间(1,2)内有一个零点x0 , g(x)为f(x)的导函数.
(Ⅰ)求g(x)的单调区间;
(Ⅱ)设m∈[1,x0)∪(x0 , 2],函数h(x)=g(x)(m﹣x0)﹣f(m),求证:h(m)h(x0)<0;
(Ⅲ)求证:存在大于0的常数A,使得对于任意的正整数p,q,且 ![]() ∈[1,x0)∪(x0 , 2],满足|
∈[1,x0)∪(x0 , 2],满足| ![]() ﹣x0|≥
﹣x0|≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设海拔x m处的大气压强是 y Pa,y与 x 之间的函数关系式是 y=cekx,其中c,k为常量,已知某地某天在海平面的大气压为1.01×105 Pa,1 000 m高空的大气压为0.90×105 Pa,求600 m高空的大气压强(精确到0.001).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com