(1)证明:连接AD
1,
∵C
1C⊥面ABCD,D
1D⊥面ABCD,
∴C
1C∥D
1D,
∵C
1C=D
1D=2,
∴四边形C
1D
1AE为平行四边形,
∴EC
1∥AD
1,
∵EC
1?面AA
1D
1D,AD
1?面AA
1D
1D,
∴EC
1∥面AA
1D
1D.
(2)连接ED,则四边形EBCD为平行四边形,
当BC=2时,BC=BE,
平行四边形EBCD为菱形,
∴EC⊥BD,
∵B
1B⊥面ABCD,B
1B⊥EC,又B
1B∩BD=B,
∴EC⊥面B
1BDD
1,
∴面C
1EC⊥面B
lBDD
l.
(3)延长BC,B
1C
1,交于点P,则
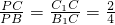
,
∴PC=
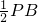
,∵BC=2,∴PC=2,
延长AD交BC于点P′.
同理,
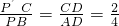
,
∴

,
∴点P与点P‘重合,
∴BC,B
1C
1,AD延长线交于一点P,
同理,BC,B
1C
1,A
1D
1,AD延长线相交于同一点P,
过点P作直线l∥CD,则l为面ABCD和面A
1B
1C
1D
1的交线,
取A
1B
1中点F,连接EF,EP,FP,
∴PB=PA=4,
E为AB中点,
∴PE⊥AB,∴PE⊥l,
同理,PF⊥l,∠EPF为二面角A-l-A
1的平面角,
在Rt△PEF中,PE=

=

,
EF=BB
1=4,
∴tan∠EPF=
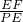
=
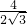
=

.
分析:(1)连接AD
1,由C
1C⊥面ABCD,知D
1D⊥面ABCD,所以C
1C∥D
1D,由C
1C=D
1D=2,知四边形C
1D
1AE为平行四边形,由此能证明EC
1∥面AA
1D
1D.
(2)连接ED,则四边形EBCD为平行四边形,当BC=2时,BC=BE,平行四边形EBCD为菱形,所以EC⊥BD,由B
1B⊥面ABCD,B
1B⊥EC,能证明面C
1EC⊥面B
lBDD
l.
(3)延长BC,B
1C
1,交于点P,则
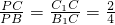
,故PC=2,延长AD交BC于点P′.同理,
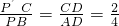
,故

,故点P与点P‘重合,BC,B
1C
1,AD延长线交于一点P,同理,BC,B
1C
1,A
1D
1,AD延长线相交于同一点P,由此入手能够求出tan∠EPF的值.
点评:本题考查二面角的平面角及其求法,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

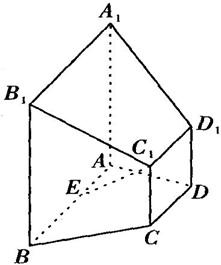 如图,在多面体ABCD-A1B1C1D1中,四边形ABCD为等腰梯形,且AB∥CD,棱AA1,BB1,CCl,DDl垂直于面ABCD,AB=4,CD=2,CC1=DDl=2,BBl=AAl=4,E为AB的中点.
如图,在多面体ABCD-A1B1C1D1中,四边形ABCD为等腰梯形,且AB∥CD,棱AA1,BB1,CCl,DDl垂直于面ABCD,AB=4,CD=2,CC1=DDl=2,BBl=AAl=4,E为AB的中点.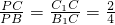 ,
,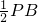 ,∵BC=2,∴PC=2,
,∵BC=2,∴PC=2,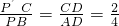 ,
, ,
, =
= ,
,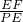 =
=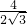 =
= .
.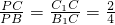 ,故PC=2,延长AD交BC于点P′.同理,
,故PC=2,延长AD交BC于点P′.同理,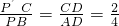 ,故
,故 ,故点P与点P‘重合,BC,B1C1,AD延长线交于一点P,同理,BC,B1C1,A1D1,AD延长线相交于同一点P,由此入手能够求出tan∠EPF的值.
,故点P与点P‘重合,BC,B1C1,AD延长线交于一点P,同理,BC,B1C1,A1D1,AD延长线相交于同一点P,由此入手能够求出tan∠EPF的值.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC= (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1= (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=