
解答题:应写出文字说明,演算步骤或证明过程
如下图,在直三棱柱ABC—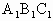 中,AC=BC=
中,AC=BC=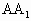 =2,∠ACB=
=2,∠ACB=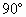 ,E、F、G分别为AC、
,E、F、G分别为AC、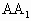 、AB的中点,
、AB的中点,
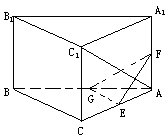
(Ⅰ)求证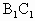 ∥平面EFG;
∥平面EFG;
(Ⅱ)求FG与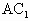 所成的角;
所成的角;
(Ⅲ)求证:FG⊥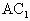 ;
;
(Ⅳ)求三棱锥 —EFG的体积.
—EFG的体积.
|
(Ⅰ)证明在直三棱柱ABC- 又已知E、G分别为AC、AB的中点,故EG为△ABC的中位线. ∴BC∥EG. ∴ 又∵EG ∴ (Ⅱ)(Ⅲ)直三棱柱ABC— 而EG ∴EG⊥ 又已知∠ACB= ∵EG∥BC, 故EG⊥AC. 由于AC∩ ∴EG⊥侧面 ∵ ∴EG⊥ 又已知AC= ∵E、F分别为AC、 据平面几何知识,得EF⊥ 由于EG∩EF=E,EGÌ 平面EFG,EFÌ 平面EFG, ∴ ∵FGÌ 平面EFG, ∴ 故 (Ⅳ)∵ ∴ 又∵ ∴
|


科目:高中数学 来源:2002年全国各省市高考模拟试题汇编 题型:044
解答题:应写出文字说明、证明过程或演算步骤
已知|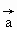 |=1,|
|=1,|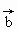 |=2,
|=2,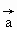 、
、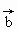 的夹角为
的夹角为![]() ,
,
(Ⅰ)求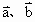 ;
;
(Ⅱ)求使向量![]() 的夹角是钝角时λ的取值范围.
的夹角是钝角时λ的取值范围.
查看答案和解析>>
科目:高中数学 来源:2002年全国各省市高考模拟试题汇编 题型:044
解答题:应写出文字说明、证明过程或演算步骤
某地在抗洪抢险中接到预报,24小时后有一个超历史最高水位的洪峰到达,为保证万无一失,抗洪指挥部决定在24小时内筑起一道堤作为第二道防线,经计算,如果有25辆大型翻斗车同时作业20小时可以筑起第二道防线,但是除了现有的一辆车可以立即投入作业外,其余车辆需从各处紧急抽调,每隔20分钟就有一辆车到达并投入工作,问指挥部至少还需组织多少辆车这样陆续工作,才能保证24小时内完成第二道防堤,请说明理由.
查看答案和解析>>
科目:高中数学 来源:广东省惠州市2007届高三第一次调研考试数学试题(文科卷) 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源:广东省惠州市2007届高三第一次调研考试数学试题(文科卷) 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:2011年全国新课标普通高等学校招生统一考试文科数学 题型:解答题
三.解答题(解答应写出文字说明,证明过程或演算步骤):
17. (本小题满分12分)
已知等比数列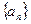 中,
中,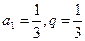 ,
,
(1)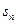 为数列
为数列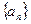 前
前 项的和,证明:
项的和,证明:
(2)设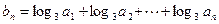 ,求数列
,求数列 的通项公式;
的通项公式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com