
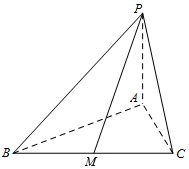
 在三棱锥P-ABC中,底面ABC是边长为6的正三角形,PA⊥底面ABC,且PB与底面ABC所成的角为$\frac{π}{6}$.
在三棱锥P-ABC中,底面ABC是边长为6的正三角形,PA⊥底面ABC,且PB与底面ABC所成的角为$\frac{π}{6}$.分析 (1)在Rt△PAB中计算PA,再代入棱锥的体积公式计算;
(2)取棱AC的中点N,连接MN,NP,分别求出△PMN的三边长,利用余弦定理计算cos∠PMN即可.
解答 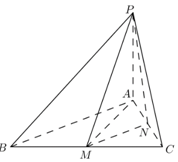 解:(1)∵PA⊥平面ABC,
解:(1)∵PA⊥平面ABC,
∴∠PBA为PB与平面ABC所成的角,即$∠PBA=\frac{π}{6}$,
∵PA⊥平面ABC,∴PA⊥AB,又AB=6,∴$PA=2\sqrt{3}$,
∴${V_{P-ABC}}=\frac{1}{3}{S_{△ABC}}•PA=\frac{1}{3}•\frac{{\sqrt{3}}}{4}•{6^2}•2\sqrt{3}=18$.
(2)取棱AC的中点N,连接MN,NP,
∵M,N分别是棱BC,AC的中点,
∴MN∥BA,∴∠PMN为异面直线PM与AB所成的角.
∵PA⊥平面ABC,所以PA⊥AM,PA⊥AN,
又$MN=\frac{1}{2}AB=3$,AN=$\frac{1}{2}$AC=3,BM=$\frac{1}{2}$BC=3,
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=3$\sqrt{3}$,$PN=\sqrt{P{A^2}+A{N^2}}=\sqrt{21}$,$PM=\sqrt{P{A^2}+A{M^2}}=\sqrt{39}$,
所以$cos∠PMN=\frac{{M{P^2}+M{N^2}-P{N^2}}}{2MP•MN}=\frac{{3\sqrt{39}}}{26}$,
故异面直线PM与AB所成的角为$arccos\frac{{3\sqrt{39}}}{26}$.
点评 本题考查了棱锥的体积计算,空间角的计算,属于中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 截两坐标轴所得弦的长度相等 | B. | 与两坐标轴都相切 | ||
| C. | 与两坐标轴相离 | D. | 上述情况都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 80 | B. | 120 | C. | 160 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
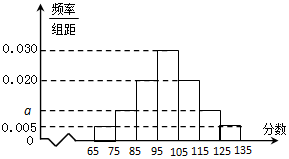 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com