
【题目】已知函数f(x)= ![]() ,若函数g(x)=f2(x)﹣axf(x)恰有6个零点,则a的取值范围是( )
,若函数g(x)=f2(x)﹣axf(x)恰有6个零点,则a的取值范围是( )
A.(0,3)
B.(1,3)
C.(2,3)
D.(0,2)
科目:高中数学 来源: 题型:
【题目】(本题满分10分)已知等差数列{an}满足a1+a2=10,a4-a3=2.
(1)求{an}的通项公式.
(2)设等比数列{bn}满足b2=a3,b3=a7.问:b6与数列{an}的第几项相等?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如下:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
芯片甲 | 8 | 12 | 40 | 32 | 8 |
芯片乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计芯片甲,芯片乙为合格品的概率;
(2)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(1)的前提下,记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列及生产1件芯片甲和1件芯片乙所得总利润的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
(α为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为 ![]() .
.
(1)求C的普通方程和l的倾斜角;
(2)设点P(0,2),l和C交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
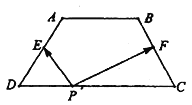
【题目】如图,梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和![]() 分别为
分别为![]() 与
与![]() 的中点,对于常数
的中点,对于常数![]() ,在梯形
,在梯形![]() 的四条边上恰好有8个不同的点
的四条边上恰好有8个不同的点![]() ,使得
,使得![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学得到方程2x+e﹣0.3x﹣100=0(其中e=2.7182…)的大于零的近似解依次为①50;②50.1;③49.5;④50.001,你认为的答案为最佳近似解(请填甲、乙、丙、丁中的一个)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为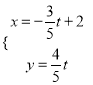 (
(![]() 为参数).
为参数).
(Ⅰ)若![]() ,
, ![]() 是直线
是直线![]() 与
与![]() 轴的交点,
轴的交点, ![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(Ⅱ)若直线![]() 被圆
被圆![]() 截得的弦长等于圆
截得的弦长等于圆![]() 的半径
的半径![]() 倍,求
倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知.f(x)=sinxcosx-![]() cos2x+
cos2x+![]()
(1)求f(x)的最小正周期,并求其图象对称中心的坐标;
(2)当0≤x≤![]() 时,求函数f(x)的值域.
时,求函数f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com