
分析 利用公式${a}^{\frac{m}{n}=\root{n}{{a}^{m}}}$,结合分数指数幂的性质和运算法则求解.
解答 解:(1)$\root{4}{81×\sqrt{{9}^{\frac{2}{3}}}}$=$8{1}^{\frac{1}{4}}×{9}^{\frac{1}{12}}$=3×${3}^{\frac{1}{6}}$=${3}^{\frac{7}{6}}$.
(2)2$\sqrt{3}$×$\root{3}{1.5}$×$\root{6}{12}$=$2×{3}^{\frac{1}{2}}×\frac{{3}^{\frac{1}{3}}}{{2}^{\frac{1}{3}}}×{3}^{\frac{1}{6}}×{2}^{\frac{1}{3}}$=2×3=6.
(3)0.0001${\;}^{-\frac{1}{4}}$+27${\;}^{\frac{2}{3}}$-($\frac{49}{64}$)${\;}^{-\frac{1}{2}}$+($\frac{1}{9}$)-1.5
=(10-4)${\;}^{-\frac{1}{4}}$+(33)${\;}^{\frac{2}{3}}$-[($\frac{7}{8}$)2]${\;}^{-\frac{1}{2}}$+[($\frac{1}{3}$)2]${\;}^{-\frac{3}{2}}$
=10+9-$\frac{8}{7}$+27
=$\frac{314}{7}$.
点评 本题考查有理数指数幂的化简求值,是基础题,解题时要认真审题,注意分数指数幂的性质和运算法则的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{12},0$)对称 | |
| B. | 可由函数f(x)的图象向右平移$\frac{π}{3}$个单位得到 | |
| C. | 可由函数f(x)的图象向左平移$\frac{π}{6}$个单位得到 | |
| D. | 可由函数f(-x)的图象向右平移$\frac{π}{12}$个单位得到 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
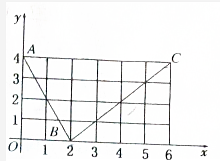 如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).
如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | logba<logab<logb$\frac{b}{a}$ | B. | logb$\frac{b}{a}$<logba<logab | ||
| C. | logba<logb$\frac{b}{a}$<logab | D. | logab<logb$\frac{b}{a}$<logba |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com