
【题目】已知点P(x,y)在△ABC的边界和内部运动,其中A(1,0),B(2,1),C(4,4).若z=2x-y的最小值为M,最大值为N.
(1)求M,N;
(2)若m+n=M,m>0,n>0,求![]() 的最小值,并求此时的m,n的值;
的最小值,并求此时的m,n的值;
(3)若m+n+mn=N,m>0,n>0,求mn的最大值和m+n的最小值.
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面ABCD为菱形,PA⊥平面ABCD,E为PD的中点.
中,底面ABCD为菱形,PA⊥平面ABCD,E为PD的中点.
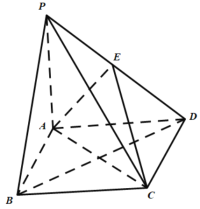
(1)求证:PB∥平面AEC;
(2)求证:平面PAC⊥平面PBD;
(3)当PA=AB=2,∠ABC=![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)设![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式.
,求证:数列{bn}是等差数列,并求出{an}的通项公式.
(2)设![]() ,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得
,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得![]() 对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的 PK 赛,![]() 两队各由 4 名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为
两队各由 4 名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为![]() ,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有甲乙两个车间,每个车间各有3台机器.甲车间每台机器每天发生故障的概率均为![]() ,乙车间3台机器每天发生概率分别为
,乙车间3台机器每天发生概率分别为![]() .若一天内同一车间的机器都不发生故障可获利2万元,恰有一台机器发生故障仍可获利1万元,恰有两台机器发生故障的利润为0万元,三台机器发生故障要亏损3万元.
.若一天内同一车间的机器都不发生故障可获利2万元,恰有一台机器发生故障仍可获利1万元,恰有两台机器发生故障的利润为0万元,三台机器发生故障要亏损3万元.
(1)求乙车间每天机器发生故障的台数的分布列;
(2)由于节能减排,甲乙两个车间必须停产一个,以工厂获得利润的期望值为决策依据,你认为哪个车间停产比较合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l经过定点P(3,5),倾斜角为
(θ为参数),直线l经过定点P(3,5),倾斜角为![]() .
.
(1)写出直线l的参数方程和曲线C的标准方程.
(2)设直线l与曲线C相交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com