
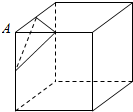
 如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 原来的六个面还在只不过是变成了一个小正方形,再添了八个顶点各对应的一个三角形的面,由此能求出面的个数;每个正方形4条边,每个三角形3条边,考虑到每条边对应两个面,由此能求出棱的条数;所有的顶点都出现在原来正方体的棱的中点位置,原来的棱的数目是12,所以现在的顶点的数目是12,由此能求出顶点数;三角形和四边形的边长都是$\frac{\sqrt{2}}{2}a$,由此求出正方形总面积、三角形总面积,从而能求出表面积;体积为原正方形体积减去8个三棱锥体积,由此能求出剩余总体积.
解答 解:如图,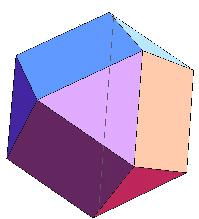 原来的六个面还在只不过是变成了一个小正方形,
原来的六个面还在只不过是变成了一个小正方形,
再添了八个顶点各对应的一个三角形的面,
所以总计6+8=14个面,故③正确;
每个正方形4条边,每个三角形3条边,4×6+3×8=48,
考虑到每条边对应两个面,所以实际只有$\frac{1}{2}×$48=24条棱.故②错误;
所有的顶点都出现在原来正方体的棱的中点位置,
原来的棱的数目是12,所以现在的顶点的数目是12.
或者从图片上可以看出每个顶点对应4条棱,每条棱很明显对应两个顶点,
所以顶点数是棱数的一半即12个.故①错误;
三角形和四边形的边长都是$\frac{\sqrt{2}}{2}a$,
所以正方形总面积为6×$\frac{1}{2}$a2=3a2,三角形总面积为8×$\frac{1}{2}×\frac{1}{2}$a2sin60°=$\sqrt{3}$a2,
表面积(3+$\sqrt{3}$)a2,故④错;
体积为原正方形体积减去8个三棱锥体积,每个三棱锥体积为8×$\frac{1}{6}$($\frac{a}{2}$)3=$\frac{1}{6}$a3,剩余总体积为a3-$\frac{1}{6}$a3=$\frac{5}{6}$a3.⑤正确.
故选:B.
点评 本题考查多面体的顶点个数、棱的条数、面的个数、表面积和体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
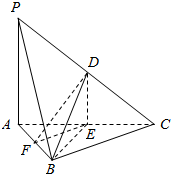 如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com