【题目】在某大学联盟的自主招生考试中，报考文史专业的考生参加了人文基础学科考试科目“语文”和“数学”的考试.某考场考生的两科考试成绩数据统计如下图所示，本次考试中成绩在
内的记为
，其中“语文”科目成绩在
内的考生有10人.
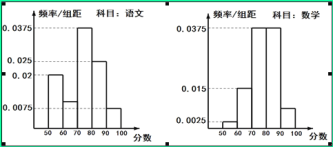
（1）求该考场考生数学科目成绩为的人数；
（2）已知参加本考场测试的考生中，恰有2人的两科成绩均为.在至少一科成绩为的考生中，随机抽取2人进行访谈，求这2人的两科成绩均为的概率.
【答案】(1)3;(2)
.
【解析】
试题分析：(1)频率分布直方图中面积表示频率，设频率=
,
为总人数，所以
，结合
的频率，
；
(2)首先算出语文与数学中成绩为
的人数，通过列举的方法计算出选出的2人所有可能的情况及这两人的两科成绩等级均为
的情况；利用古典概型概率公式求出随机抽取两人进行访谈，这两人的两科成绩等级均为的概率。
试题解析：（1）该考场的考生人数为10÷0.25=40人. 2分
数学科目成绩为
的人数为
40×(1-0.0025×10-0.015×10-0.0375×10×2)=40×0.075=3人. 6分
（2）语文和数学成绩为A的各有3人，其中有两人的两科成绩均为，所以还有两名同学只有一科成绩为. 8分
设这四人为甲、乙、丙、丁，其中甲、乙的两科成绩均为，则在至少一科成绩为的考生中，随机抽取两人进行访谈，基本事件为{甲，乙}，{甲，丙}，{甲，丁}，{乙，丙}，{乙，丁}， {丙，丁}共6个， 10分
设“随机抽取两人，这两人的两科成绩均为”为事件
，则事件包含的事件有1个，则
. 12分
智慧小复习系列答案科目：高中数学 来源： 题型：
【题目】已知圆
的圆心在直线
上，且与直线
相切于点
，
（1）求圆
方程；
（2）是否存在过点
的直线
与圆
交于
两点，且
的面积是
（
为坐标原点），若存在，求出直线
的方程，若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）的定义域是（0，+∞），且满足f（xy）=f（x）+f（y），当x＞1时，有f（x）＞0．
（1）求f（1），判定并证明f（x）的单调性；
（2）若f（2）=1，解不等式f（﹣x）+f（3﹣x）≥﹣2．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校上学期的期中考试后，为了了解某学科的考试成绩，根据学生的考试成绩利用分层抽样抽取
名学生的成绩进行统计（所有学生成绩均不低于
分），得到学生成绩的频率分布直方图如图，回答下列问题；
（Ⅰ）根据频率分布直方图计算本次考试成绩的平均分；
（Ⅱ）已知本次全校考试成绩在
内的人数为
，试确定全校的总人数；
（Ⅲ）若本次考试抽查的
人中考试成绩在
内的有
名女生，其余为男生，从中选择两名学生，求选择一名男生与一名女生的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知二次函数f（x）=ax2+bx+1，a，b∈R，当x=﹣1时，函数f（x）取到最小值，且最小值为0；
（1）求f（x）解析式；
（2）关于x的方程f（x）=|x+1|﹣k+3恰有两个不相等的实数解，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】运货卡车以每小时x千米的速度匀速行驶130千米，按交通法规限制50≤x≤100（单位：千米/时）．假设汽油的价格是每升2元，而汽车每小时耗油
升，司机的工资是每小时14元．
（1）求这次行车总费用y关于x的表达式；
（2）当x为何值时，这次行车的总费用最低，并求出最低费用的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图如下图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a，b的值分别为 ( )
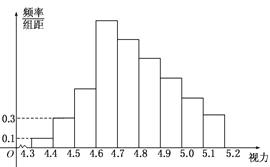
A. 0.27,78 B. 0.27,83 C. 2.7,78 D. 2.7,83
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
