
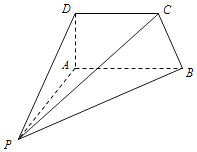
【题目】如图,四棱锥P﹣ABCD中,AD⊥平面PAB,AP⊥AB. 
(1)求证:CD⊥AP;
(2)若CD⊥PD,求证:CD∥平面PAB.
【答案】
(1)证明:因为AD⊥平面PAB,AP平面PAB,所以AD⊥AP.
又因为AP⊥AB,AB∩AD=A,AB平面ABCD,AD平面ABCD,
所以AP⊥平面ABCD.
因为CD平面ABCD,所以CD⊥AP
(2)证明:因为CD⊥AP,CD⊥PD,且PD∩AP=P,PD平面PAD,AP平面PAD,
所以CD⊥平面PAD.①
因为AD⊥平面PAB,AB平面PAB,所以AB⊥AD.
又因为AP⊥AB,AP∩AD=A,AP平面PAD,AD平面PAD,
所以AB⊥平面PAD.②
由①②得CD∥AB,
因为CD平面PAB,AB平面PAB,所以CD∥平面PAB
【解析】(1)推导出AD⊥AP,AP⊥AB,从而AP⊥平面ABCD,由此能证明CD⊥AP.(2)由CD⊥AP,CD⊥PD,得CD⊥平面PAD.再推导出AB⊥AD,AP⊥AB,从而AB⊥平面PAD,进而CD∥AB,由此能证明CD∥平面PAB.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为 ![]() ,各局比赛的结果都相互独立,第1局甲当裁判.
,各局比赛的结果都相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)X表示前4局中乙当裁判的次数,求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将边长为1的正方形![]() 沿对角线
沿对角线![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,在折起后形成的三棱锥
,在折起后形成的三棱锥![]() 中,给出下列四种说法:
中,给出下列四种说法:
①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ;④直线
;④直线![]() 和
和![]() 所成的角的大小为
所成的角的大小为![]() .其中所有正确的序号是( )
.其中所有正确的序号是( )

A. ①③B. ②④C. ①②③D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是美籍法国数学家伯努瓦.![]() .曼德尔布罗特在20世纪70年代创立的一门新学科,它的创立,为解决传统科学众多领域的难题提供了全新的思路,如图是按照一定的分形规律生产成一个数形图,则第13行的实心圆点的个数是______.
.曼德尔布罗特在20世纪70年代创立的一门新学科,它的创立,为解决传统科学众多领域的难题提供了全新的思路,如图是按照一定的分形规律生产成一个数形图,则第13行的实心圆点的个数是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假定某射手射击一次命中目标的概率为![]() .现有4发子弹,该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,求:
.现有4发子弹,该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,求:
(1)X的概率分布;
(2)数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
, ![]() 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
(2)若![]() ,
, ![]() 都是从区间
都是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 成立的概率.
成立的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC= ![]() ,E,F分别是BC,A1C的中点.
,E,F分别是BC,A1C的中点. 
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, ![]() =λ.若CM∥平面AEF,求实数λ的值.
=λ.若CM∥平面AEF,求实数λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com