
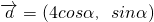 ,
,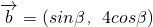 ,
,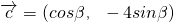 ,
,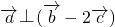 ,求tan(α+β)的值
,求tan(α+β)的值 .
.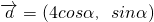 ,
,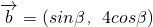 ,
,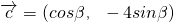 ,
,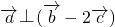 ,所以
,所以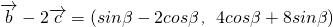 ,
,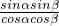 =16,
=16, 成立.命题得证
成立.命题得证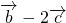 ,通过
,通过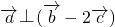 ,数量积为0,求tan(α+β)的值
,数量积为0,求tan(α+β)的值 .
.

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源:2012-2013学年山东省临沂市沂南一中高三(上)第二次质量检测数学试卷(理科)(解析版) 题型:解答题
 ,
, ,
, .
. ∥
∥ ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形; ⊥
⊥ ,边长c=2,角C=
,边长c=2,角C= ,求△ABC的面积.
,求△ABC的面积.查看答案和解析>>
科目:高中数学 来源:《8.3 平面向量的数量积及平面向量应用举例》2013年高考数学优化训练(文科)(解析版) 题型:解答题
 ,
, ,
, .
. ∥
∥ ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形; ⊥
⊥ ,边长c=2,角C=
,边长c=2,角C= ,求△ABC的面积.
,求△ABC的面积.查看答案和解析>>
科目:高中数学 来源:2013年陕西省西安市西工大附中高考数学三模试卷(文科)(解析版) 题型:解答题
 ,
, ,
, .
. ∥
∥ ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形; ⊥
⊥ ,边长c=2,角C=
,边长c=2,角C= ,求△ABC的面积.
,求△ABC的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com