
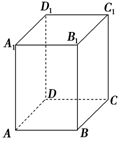
 如图,长方体ABCD-A1B1C1D1中,AB=3,BC=4,CC1=5,则沿着长方体表面从A到C1的最短路线长为$\sqrt{74}$.
如图,长方体ABCD-A1B1C1D1中,AB=3,BC=4,CC1=5,则沿着长方体表面从A到C1的最短路线长为$\sqrt{74}$. 分析 按三种不同方式展开长方体的侧面,计算平面图形中三条线段的长,比较得结论.
解答 解:长方体ABCD-A1B1C1D1的表面可如图三种方法展开后,A、C1两点间的距离分别为: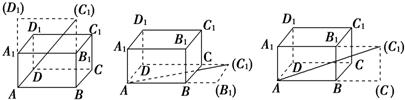
$\sqrt{{3}^{2}+(4+5)^{2}}$=3$\sqrt{10}$,
$\sqrt{{4}^{2}+(3+5)^{2}}$=4$\sqrt{5}$,
$\sqrt{{5}^{2}+(3+4)^{2}}$=$\sqrt{74}$.
三者比较得$\sqrt{74}$是从点A沿表面到C1的最短距离.
故答案为$\sqrt{74}$
点评 本题考查棱柱的结构特征,考查分类讨论思想,考查计算能力,属于中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
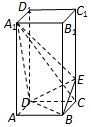 如图,在长方体ABCD-A1B1C1B1中,AA1=2AB=2AD=4,点E在CC1上且C1E=3EC.利用空间向量解决下列问题:
如图,在长方体ABCD-A1B1C1B1中,AA1=2AB=2AD=4,点E在CC1上且C1E=3EC.利用空间向量解决下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com