
��֪���� ����
����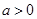 ����
����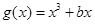
��1��������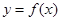 ������
������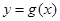 �����ǵĽ��㣨1��c�������й������ߣ���a,b��ֵ
�����ǵĽ��㣨1��c�������й������ߣ���a,b��ֵ
��2����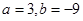 ʱ��������
ʱ��������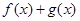 ������[k,2]�ϵ����ֵΪ28����k��ȡֵ��Χ
������[k,2]�ϵ����ֵΪ28����k��ȡֵ��Χ
����������1��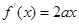 ��
��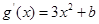
������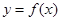 ������
������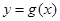 �����ǵĽ��㣨1��c�������й�������
�����ǵĽ��㣨1��c�������й�������
��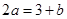 ��
��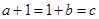
��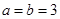
��2����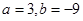 ʱ��
ʱ��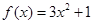 ��
��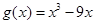 ��
��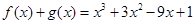
�� ����
����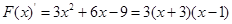 ����
����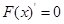 ��
�� ��
��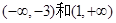 Ϊ�����������䣬
Ϊ�����������䣬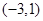 Ϊ�����ݼ����䣬����F��-3��=28Ϊ����ֵ�������������[k,2]���ֵΪ28���������������ֵ��
Ϊ�����ݼ����䣬����F��-3��=28Ϊ����ֵ�������������[k,2]���ֵΪ28���������������ֵ��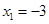 ������
������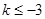
�����㶨λ������Ӧ��˵�ǵ�����Ŀ�н�Ϊ�����������Ŀ����������ߣ������ԣ���ֵ�Լ���ֵ���ⶼ�ǿα���Ҫ����ص����ݣ�Ҳ��ѧ�����ձȽϺõ�֪ʶ�㣬����Ŀ���ܹ�����F��-3��=28���ͷ���������[k,2]��������ֵ��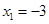 ���Ƚ���Ҫ
���Ƚ���Ҫ
 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| �� |
| 24 |
| 5�� |
| 24 |
| �� |
| 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 11�� |
| 6 |
| ||
| 2 |
| 3 |
| �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| xn+2 | xn-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|��
��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|��| �� |
| 2 |
A��f(x)=2sin(
| ||||
B��f(x)=2sin(
| ||||
C��f(x)=2sin(2x-
| ||||
D��f(x)=2sin(2x+
|
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com