
| A. | $\frac{3}{2}$ | B. | $-\frac{4}{3}$ | C. | $-\frac{3}{2}$ | D. | $-\frac{5}{2}$ |
分析 推导出{an}有连续四项在{-54,-24,18,36,81}中,从而q<0,且负数项为相隔两项等比数列各项的绝对值递增,按绝对值的顺序排列上述数值,由此能示出结果.
解答 解:数列{bn}有连续四项在集合{-53,-23,19,37,82}中,
且bn=an+1(n∈N*),∴an=bn-1,
则{an}有连续四项在{-54,-24,18,36,81}中,
∵数列{an}是公比为q(|q|>1)的等比数列,
等比数列中有负数项,则q<0,且负数项为相隔两项
∵|q|>1,∴等比数列各项的绝对值递增,按绝对值的顺序排列上述数值18,-24,36,-54,81,
相邻两项相除$\frac{-24}{18}$=-$\frac{4}{3}$,$\frac{-36}{24}$=-$\frac{3}{2}$,$\frac{-54}{36}$=-$\frac{3}{2}$,$\frac{81}{-54}$=-$\frac{3}{2}$,
∵|q|>1,∴-24,36,-54,81是{an}中连续的四项,此时q=-$\frac{3}{2}$.
故选:C.
点评 本题考查等比数列的公比的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
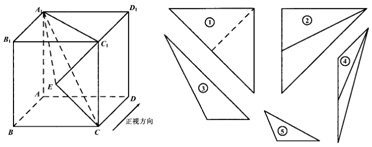
| A. | ①和⑤ | B. | ②和③ | C. | ④和⑤ | D. | ④和③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\sqrt{6}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -$\frac{1}{6}$ | C. | $\frac{1}{6}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 空间几何体ABCDEF如图所示.已知面ABCD⊥面ADEF,ABCD为梯形,ADEF为正方形,且AB∥CD,AB⊥AD,CD=4,AB=AD=2,G为CE的中点.
空间几何体ABCDEF如图所示.已知面ABCD⊥面ADEF,ABCD为梯形,ADEF为正方形,且AB∥CD,AB⊥AD,CD=4,AB=AD=2,G为CE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com