练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，半径为 的扇形AOB的圆心角为120°，点C在 上，且∠COB=30°，若 ，则λ+μ=

    【答案】
    【解析】解：如图所示，建立直角坐标系．
    ∵∠BOC=30°，OC= ．
    ∴C（ cos30°， sin30°），
    即C（ ， ）．
    ∵∠BOA=120°，
    ∴A（ cos120°， sin120°），
    即A（﹣ ， ）．
    又B（ ，0），
    ，
    ∴（ ， ）=λ（﹣ ， ）+μ（ ，0）．
    ∴ ，解得 ．
    ∴λ+μ= ．
    所以答案是：

    【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点，需要掌握如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

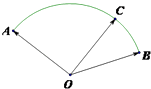
    科目：高中数学 来源： 题型：

    【题目】已知O为坐标原点，P（x，y）为函数y=1+lnx图象上一点，记直线OP的斜率k=f（x）． （Ⅰ）若函数f（x）在区间（m，m+ ）（m＞0）上存在极值，求实数m的取值范围；
    （Ⅱ）当x≥1时，不等式f（x）≥ 恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四种说法中，
    ①命题“存在x∈R，x2﹣x＞0”的否定是“对于任意x∈R，x2﹣x＜0”；
    ②命题“p且q为真”是“p或q为真”的必要不充分条件；
    ③已知幂函数f（x）=xα的图象经过点（2， ），则f（4）的值等于 ；
    ④已知向量 =（3，﹣4）， =（2，1），则向量 在向量 方向上的投影是 ．
    说法错误的个数是（ ）
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工艺品厂要设计一个如图Ⅰ所示的工艺品，现有某种型号的长方形材料如图Ⅱ所示，其周长为4m，这种材料沿其对角线折叠后就出现图Ⅰ的情况．如图，ABCD（AB＞AD）为长方形的材料，沿AC折叠后AB'交DC于点P，设△ADP的面积为
    S2 ， 折叠后重合部分△ACP的面积为S1 ．
    （Ⅰ）设AB=xm，用x表示图中DP的长度，并写出x的取值范围；
    （Ⅱ）求面积S2最大时，应怎样设计材料的长和宽？
    （Ⅲ）求面积（S1+2S2）最大时，应怎样设计材料的长和宽？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2sinωx，其中常数ω＞0．
    （Ⅰ）令ω=1，求函数 在 上的最大值；
    （Ⅱ）若函数 的周期为π，求函数g（x）的单调递增区间，并直接写出g（x）在 的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某软件公司新开发一款学习软件，该软件把学科知识设计为由易到难共12关的闯关游戏．为了激发闯关热情，每闯过一关都奖励若干慧币（一种网络虚拟币）．该软件提供了三种奖励方案：第一种，每闯过一关奖励40慧币；第二种，闯过第一关奖励4慧币，以后每一关比前一关多奖励4慧币；第三种，闯过第一关奖励0.5慧币，以后每一关比前一关奖励翻一番（即增加1倍），游戏规定：闯关者须于闯关前任选一种奖励方案．
    （Ⅰ）设闯过n （ n∈N，且n≤12）关后三种奖励方案获得的慧币依次为An ， Bn ， Cn ， 试求出An ， Bn ， Cn的表达式；
    （Ⅱ）如果你是一名闯关者，为了得到更多的慧币，你应如何选择奖励方案？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在高中学习过程中，同学们经常这样说：“数学物理不分家，如果物理成绩好，那么学习数学就没什么问题．”某班针对“高中生物理学习对数学学习的影响”进行研究，得到了苏俄生的物理成绩与数学成绩具有线性相关关系的结论．现从该班随机抽取5名学生在一次考试中的数学和物理成绩，如表：

    成绩 编号

    1

    2

    3

    4

    5

    物理（x）

    90

    85

    74

    68

    63

    数学（y）

    130

    125

    110

    95

    90


    （1）求数学成绩y对物理成绩x的线性回归方程 = x+ （ 精确到0.1）．若某位学生的物理成绩为80分，预测他的数学成绩；
    （2）要从抽取的这五位学生中随机选出2位参加一项知识竞赛，求选中的学生的数学成绩至少有一位高于120分的概率．（参考公式： = ， = ﹣ ） （参考数据：902+852+742+682+632=29394，90××125+74×110+68×95+63×90=42595）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】由于研究性学习的需要，中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数，其中某一天的数据记录如下： 5860 6520 7326 6798 7325
    8430 8215 7453 7446 6754
    7638 6834 6460 6830 9860
    8753 9450 9860 7290 7850
    对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：
    步数分组统计表（设步数为x）

    组别

    步数分组

    频数

    A

    5500≤x＜6500

    2

    B

    6500≤x＜7500

    10

    C

    7500≤x＜8500

    m

    D

    8500≤x＜9500

    2

    E

    9500≤x＜10500

    n

    （Ⅰ）写出m，n的值，并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别；
    （Ⅱ）记C组步数数据的平均数与方差分别为v1 ， ，E组步数数据的平均数与方差分别为v2 ， ，试分别比较v1与v2 ， 与 的大小；（只需写出结论）
    （Ⅲ）从上述A，E两个组别的数据中任取2个数据，记这2个数据步数差的绝对值为ξ，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在平面四边形ABCD中，AB= ，BC=2，AC⊥CD，AC=CD，则四边形ABCD面积的最大值为 ．

    查看答案和解析>>

    同步练习册答案