
【题目】若一个四位数的各位数字相加和为10,则称该数为“完美四位数”,如数字“2017”.试问用数字0,1,2,3,4,5,6,7组成的无重复数字且大于2017的“完美四位数”有( )个.
A. 71B. 66C. 59D. 53
【答案】A
【解析】
根据题意,分析可得四位数字相加和为10的情况有①0、1、3、6,②0、1、4、5,③0、1、
2、7,④0、2、3、5,⑤1、2、3、4;共5种情况,据此分5种情况讨论,依次求出每种情
况下大于2017的“完美四位数”的个数,将其相加即可得答案.
根据题意,四位数字相加和为10的情况有①0、1、3、6,②0、1、4、5,③0、1、2、7,
④0、2、3、5,⑤1、2、3、4;共5种情况,
则分5种情况讨论:
①、四个数字为0、1、3、6时,
千位数字可以为3或6,有2种情况,将其余3个数字全排列,安排在百位、十位、个位,
有![]() 种情况,此时有
种情况,此时有![]() 个“完美四位数”,
个“完美四位数”,
②、四个数字为0、1、4、5时,
千位数字可以为4或5,有2种情况,将其余3个数字全排列,安排在百位、十位、个位,
有![]() 种情况,此时有
种情况,此时有![]() 个“完美四位数”,
个“完美四位数”,
③、四个数字为0、1、2、7时,
千位数字为7时,将其余3个数字全排列,安排在百位、十位、个位,有![]() 种情况,
种情况,
千位数字为2时,有2071、2107、2170、2701、2710,共5种情况,此时有![]() 个“完
个“完
美四位数”,
④、四个数字为0、2、3、5时,
千位数字可以为2或3或5,有3种情况,将其余3个数字全排列,安排在百位、十位、个
位,有![]() 种情况,此时有
种情况,此时有![]() 个“完美四位数”,
个“完美四位数”,
⑤、四个数字为1、2、3、4时,
千位数字可以为3或4或2,有3种情况,将其余3个数字全排列,安排在百位、十位、个
位,有![]() 种情况,此时有
种情况,此时有![]() 个“完美四位数”,
个“完美四位数”,
则一共有![]() 个“完美四位数”,
个“完美四位数”,
故选:![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,多面体 ABCDEF中,四边形ABCD是边长为2的菱形,且平面ABCD⊥平面DCE.AF∥DE,且AF=![]() DE=2,BF=2
DE=2,BF=2![]() .
.
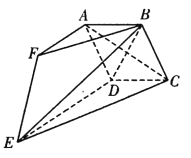
(1)求证:AC⊥BE;
(2)若点F到平面DCE的距离为![]() ,求直线EC与平面BDE所成角的正弦值.
,求直线EC与平面BDE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() (1+cos2θ)=8sinθ.
(1+cos2θ)=8sinθ.
(1)求曲线C的普通方程;
(2)直线l的参数方程为![]() ,t为参数直线
,t为参数直线![]() 与y轴交于点F与曲线C的交点为A,B,当|FA||FB|取最小值时,求直线
与y轴交于点F与曲线C的交点为A,B,当|FA||FB|取最小值时,求直线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两种棉花中各抽测了25根棉花的纤维长度(单位: ![]() ) 组成一个样本,且将纤维长度超过315
) 组成一个样本,且将纤维长度超过315![]() 的棉花定为一级棉花.设计了如下茎叶图:
的棉花定为一级棉花.设计了如下茎叶图:

(1)根据以上茎叶图,对甲、乙两种棉花的纤维长度作比较,写出两个统计结论(不必计算);
(2)从样本中随机抽取甲、乙两种棉花各2根,求其中恰有3根一级棉花的概率;
(3)用样本估计总体,将样本频率视为概率,现从甲、乙两种棉花中各随机抽取1根,求其中一级棉花根数X的分布列及数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4一4:坐标系与参数方程
在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() 参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 是圆心的极坐标为(
是圆心的极坐标为(![]() )且经过极点的圆
)且经过极点的圆
(1)求曲线C1的极坐标方程和C2的普通方程;
(2)已知射线![]() 分別与曲线C1,C2交于点A,B(点B异于坐标原点O),求线段AB的长
分別与曲线C1,C2交于点A,B(点B异于坐标原点O),求线段AB的长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N*,总有b1![]() b2
b2![]() b3…bn﹣1
b3…bn﹣1![]() bn=an+2成立.
bn=an+2成立.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=(﹣1)n![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一网购狂欢节”源于淘宝商城(天猫)![]() 年
年![]() 月
月![]() 日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是
日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是![]() 月
月![]() 日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商为分析近
日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商为分析近![]() 年“双十一”期间的宣传费用
年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,搜集了相关数据,得到下列表格:
(单位:十万元)之间的关系,搜集了相关数据,得到下列表格:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)建立![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ),预测当宣传费用为
),预测当宣传费用为![]() 万元时的利润.
万元时的利润.
附参考公式:回归方程![]() 中
中![]() 和
和![]() 最小二乘估计公式分别为
最小二乘估计公式分别为
 ,
,![]() ,相关系数
,相关系数
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.下图所示的阳马![]() 中,侧棱
中,侧棱![]() 底面ABCD,且
底面ABCD,且![]() ,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体
,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体![]() 中,鳖臑有( )个.
中,鳖臑有( )个.
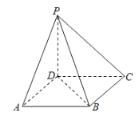
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种细菌的适宜生长温度为10℃~25℃,为了研究该种细菌的繁殖数量![]() (单位:个)随温度
(单位:个)随温度![]() (单位:℃)变化的规律,收集数据如下:
(单位:℃)变化的规律,收集数据如下:
温度 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
繁殖数量 | 20 | 25 | 33 | 27 | 51 | 112 | 194 |
对数据进行初步处理后,得到了一些统计量的值,如下表所示:
|
|
|
|
|
|
|
18 | 66 | 3.8 | 112 | 4.3 | 1428 | 20.5 |
其中![]() ,
,![]() .
.
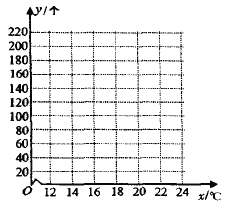
(1)请绘出![]() 关于
关于![]() 的散点图,并根据散点图判断
的散点图,并根据散点图判断![]() 与
与![]() 哪一个更适合作为该种细菌的繁殖数量
哪一个更适合作为该种细菌的繁殖数量![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表格数据,建立![]() 关于
关于![]() 的回归方程(结果精确到0.1);
的回归方程(结果精确到0.1);
(3)当温度为25℃时,该种细菌的繁殖数量的预报值为多少?
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二成估计分别为
的斜率和截距的最小二成估计分别为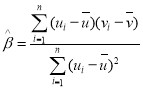 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com