
【题目】如图,在三棱锥![]() 中平面
中平面![]() 平面
平面![]() ,
,![]() .
.
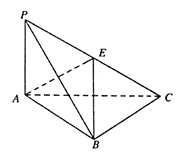
(Ⅰ)证明:![]() ;
;
(Ⅱ)若点E为![]() 中点,
中点,![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】对于函数y=H(x),若在其定义域内存在x0,使得x0·H(x0)=1成立,则称x0为函数H(x)的“倒数点”.已知函数f(x)=ln x,g(x)=![]() (x+1)2-1.
(x+1)2-1.
(1)求证:函数f(x)有“倒数点”,并讨论函数f(x)的“倒数点”的个数;
(2)若当x≥1时,不等式xf(x)≤m[g(x)-x]恒成立,试求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,若椭圆上的点与两个焦点构成的三角形中,面积最大为1.
,若椭圆上的点与两个焦点构成的三角形中,面积最大为1.
(1)求椭圆的标准方程;
(2)设直线![]() 与椭圆的交于
与椭圆的交于![]() 两点,
两点,![]() 为坐标原点,且
为坐标原点,且![]() ,证明:直线
,证明:直线![]() 与圆
与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,D(0,2)为椭圆C短轴的一个端点,F为椭圆C的右焦点,线段DF的延长线与椭圆C相交于点E,且|DF|=3|EF|.
(1)求椭圆C的标准方程;
(2)设直线l与椭圆C相交于A,B两点,O为坐标原点,若直线OA与OB的斜率之积为-![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《郑州市城市生活垃圾分类管理办法》已经政府常务会议审议通过,自2019年12月1日起施行.垃圾分类是对垃圾收集处置传统方式的改革,是对垃圾进行有效处置的一种科学管理方法.所谓垃圾其实都是资源,当你放错了位置时它才是垃圾.某企业在市科研部门的支持下进行研究,把厨余垃圾加工处理为一种可销售的产品.已知该企业每周的加工处理量最少为75吨,最多为100吨.周加工处理成本y(元)与周加工处理量x(吨)之间的函数关系可近似地表示为![]() ,且每加工处理一吨厨余垃圾得到的产品售价为16元.
,且每加工处理一吨厨余垃圾得到的产品售价为16元.
(Ⅰ)该企业每周加工处理量为多少吨时,才能使每吨产品的平均加工处理成本最低?
(Ⅱ)该企业每周能否获利?如果获利,求出利润的最大值;如果不获利,则需要市政府至少补贴多少元才能使该企业不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射手每次射击击中目标的概率是![]() ,且各次射击的结果互不影响.
,且各次射击的结果互不影响.
(Ⅰ)假设这名射手射击![]() 次,求有
次,求有![]() 次连续击中目标,另外
次连续击中目标,另外![]() 次未击中目标的概率;
次未击中目标的概率;
(Ⅱ)假设这名射手射击![]() 次,记随机变量
次,记随机变量![]() 为射手击中目标的次数,求
为射手击中目标的次数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线 (
(![]() 为参数),
为参数),![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(I)写出曲线![]() 与圆
与圆![]() 的极坐标方程;
的极坐标方程;
(II)在极坐标系中,已知射线![]() 分别与曲线
分别与曲线![]() 及圆
及圆![]() 相交于
相交于![]() ,当
,当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 |
|
|
|
|
净利润占比 |
|
|
|
|
则下列判断中不正确的是( )
A. 该公司2018年度冰箱类电器营销亏损
B. 该公司2018年度小家电类电器营业收入和净利润相同
C. 该公司2018年度净利润主要由空调类电器销售提供
D. 剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com