
【题目】已知函数![]() (其中
(其中![]() 为常数且
为常数且![]() )
)
(1)若函数![]() 为减函数,求实数
为减函数,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 有两个不同的零点,求实数
有两个不同的零点,求实数![]() 的取值范围,并说明理由.
的取值范围,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() 函数
函数![]() 为减函数,等价于
为减函数,等价于![]() ,即
,即![]() 对
对![]() 恒成立,求出
恒成立,求出![]() 的最小值即可得结果;(2)
的最小值即可得结果;(2)![]() 设
设![]() ,则原命题等价于函数
,则原命题等价于函数![]() 有两个不同的零点,分类讨论
有两个不同的零点,分类讨论![]() 的范围,分别利用导数研究函数
的范围,分别利用导数研究函数![]() 的单调性,结合函数图象与零点存在定理,可筛选出符合题意的实数
的单调性,结合函数图象与零点存在定理,可筛选出符合题意的实数![]() 的取值范围.
的取值范围.
(1)![]()
![]()
若函数![]() 为减函数,则
为减函数,则![]() ,即
,即![]() 对
对![]() 恒成立.
恒成立.
设![]()
![]() 在区间
在区间![]() 上递减
上递减![]() 递增
递增
![]() 即
即![]() 故实数
故实数![]() 的取值范围是
的取值范围是![]()
(2)易知函数![]() 的定义域为
的定义域为![]()
设![]() ,则原命题等价于函数
,则原命题等价于函数![]() 有两个不同的零点,求实数
有两个不同的零点,求实数![]() 的取值范围,
的取值范围,
![]()
![]()
![]() 当
当![]() 时,
时,![]() 函数
函数![]() 在区间
在区间![]() 上递减
上递减![]() 上递增,
上递增,![]() 若函数
若函数![]() 有两个不同的零点则必有
有两个不同的零点则必有![]() 即
即![]() 此时,在
此时,在![]() 上有
上有
![]() 在
在![]() 上,
上,![]()
![]()
![]()
![]()
![]() 在区间
在区间![]() 上各有一个零点,故
上各有一个零点,故![]() 合题意;
合题意;
当![]() 时,
时,![]() 函数
函数![]() 在区间
在区间![]() 递减,
递减,![]() 函数
函数![]() 至多一个零点,不合题意;
至多一个零点,不合题意;
当![]() 时,
时,![]() 函数
函数![]() 在区间
在区间![]() 递减、
递减、![]() 递增、
递增、![]() 递减,
递减,
![]() 函数
函数![]() 的极小值为
的极小值为![]() 函数
函数![]() 至多一个零点,不合题意;
至多一个零点,不合题意;
当![]() 时,
时,![]() 函数
函数![]() 在区间
在区间![]() 递减、
递减、![]() 递增、
递增、![]() 递减,
递减,
![]() 函数
函数![]() 的极小值为
的极小值为![]()
![]() ,
,
![]() 函数
函数![]() 至多一个零点,不合题意.
至多一个零点,不合题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 交于点P.
交于点P.
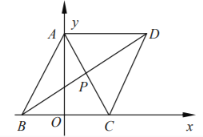
(1)求直线![]() 的方程;
的方程;
(2)若点E,F分别在平行四边形![]() 的边
的边![]() 和
和![]() 上运动,且
上运动,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)试写出三角形![]() 区域(包括边界)所满足的线性约束条件,若在该区域上任取一点M,使
区域(包括边界)所满足的线性约束条件,若在该区域上任取一点M,使![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年数学竞赛邀请了一位来自![]() 星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题目就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题,然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答得题目则跳过(例如,他可以按照9、8、7、4、3、2、1、5、6、10的次序答题),这样所有题目均有作答,则这位选手可能的答题次序有______种.
星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题目就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题,然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答得题目则跳过(例如,他可以按照9、8、7、4、3、2、1、5、6、10的次序答题),这样所有题目均有作答,则这位选手可能的答题次序有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
品牌 | 甲 | 乙 | |||
首次出现故 障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
每辆利润 (万元) | 1 | 2 | 3 | 1.8 | 2.9 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率.
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列.
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,![]() ,
,![]() ,
,![]() ,M是棱PC上一点,且
,M是棱PC上一点,且![]() ,
,![]() 平面MBD.
平面MBD.
(1)求实数λ的值;
(2)若平面![]() 平面ABCD,
平面ABCD,![]() 为等边三角形,且三棱锥P-MBD的体积为2,求PA的长.
为等边三角形,且三棱锥P-MBD的体积为2,求PA的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 为其左右焦点,
为其左右焦点,![]() 为其上下顶点,四边形
为其上下顶点,四边形![]() 的面积为
的面积为![]() .点
.点![]() 为椭圆
为椭圆![]() 上任意一点,以
上任意一点,以![]() 为圆心的圆(记为圆
为圆心的圆(记为圆![]() )总经过坐标原点
)总经过坐标原点![]() .
.
(1)求椭圆![]() 的长轴
的长轴![]() 的最小值,并确定此时椭圆
的最小值,并确定此时椭圆![]() 的方程;
的方程;
(2)对于(1)中确定的椭圆![]() ,若给定圆
,若给定圆![]() ,则圆
,则圆![]() 和圆
和圆![]() 的公共弦
的公共弦![]() 的长是否为定值?如果是,求
的长是否为定值?如果是,求![]() 的值;如果不是,请说明理由.
的值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个数列的各项是1和2,首项是1,且在第![]() 个1和第
个1和第![]() 个1之间有
个1之间有![]() 个2,即1,2,1,2,2,1,2,2,2,2,1,2,2,2,2,2,2,2,2,1…,则此数列的前2017项的和
个2,即1,2,1,2,2,1,2,2,2,2,1,2,2,2,2,2,2,2,2,1…,则此数列的前2017项的和![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班对一次实验成绩进行分析,利用随机数表法抽取样本时,先将50个同学按01,02.03,…50进行编号,然后从随机数表第9行第11列的数开始向右读,则选出的第6个个体是( )(注:表为随机数表的第8行和第9行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
A.00B.13C.42D.44
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com