
【题目】(本小题满分13分)
已知圆满足:
① 截y轴所得弦长为2;
②被x轴分成两段圆弧,其弧长的比为3:1;
③圆心到直线l:x-2y=0的距离为![]() ,求该圆的方程.
,求该圆的方程.
【答案】![]() 或
或![]()
【解析】
法一)设圆P的圆心为P(a,b),半径为r,
则点P到x轴,y轴的距离分别为|b|,|a|.
由题意可知圆P截x轴所得劣弧对的圆心角为90°
圆P截x轴所得的弦长为![]() ,2|b|=
,2|b|=![]() ,得r2=2b2, ……3分
,得r2=2b2, ……3分
圆P被y轴所截得的弦长为2,由勾股定理得r2=a2+1,
得2b2- a2=1. …………6分
又因P(a,b)到直线x -2y=0的距离为![]() ,得d=
,得d=![]() ,即有
,即有![]() …9分
…9分
综前述得![]() ,
,![]() 解得
解得![]() ,
,![]() ,于是r2= 2b2=2
,于是r2= 2b2=2
所求圆的方程是![]() ,或
,或![]() …………13分
…………13分
(法二)设圆的方程为![]() ,
,
令x =0,得![]() ,
,
所以![]() ,得
,得![]()
再令y=0,可得![]() ,
,
所以![]() ,得
,得![]() ,
,
即![]() ,从而有2b2- a2=1.
,从而有2b2- a2=1.
又因为P(a,b)到直线x -2y=0的距离为![]() ,
,
得d=![]() ,即有
,即有![]()
综前述得![]() ,
,![]() 解得
解得![]() ,
,![]() ,于是r2= 2b2=2
,于是r2= 2b2=2
所求圆的方程是![]() ,或
,或![]()


科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的斜率分别记为
的斜率分别记为![]() 与
与![]() ,且
,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过定点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点, ![]() 的面积是否存在最大值?若存在,求出
的面积是否存在最大值?若存在,求出![]() 面积的最大值;若不存在,请说明理由.
面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数f(x)= ![]() ,称为狄利克雷函数,则关于函数f(x)有以下四个命题: ①f(f(x))=1;
,称为狄利克雷函数,则关于函数f(x)有以下四个命题: ①f(f(x))=1;
②函数f(x)是偶函数;
③任意一个非零有理数T,f(x+T)=f(x)对任意x∈R恒成立;
④存在三个点A(x1 , f(x1)),B(x2 , f(x2)),C(x3 , f(x3)),使得△ABC为等边三角形.
其中真命题的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在[20,45]的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示. 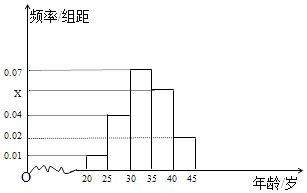
(1)求图中x的值,并根据频率分布直方图估计这500名志愿者中年龄在[35,40)岁的人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过C(1,-1),D(-1,1)两点,且圆心M在x+y-2=0上.
(1)求圆M的方程;
(2)设点P是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=aln(x2+1)+bx存在两个极值点x1 , x2 .
(1)求证:|x1+x2|>2;
(2)若实数λ满足等式f(x1)+f(x2)+a+λb=0,试求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中是错误命题的个数有( )
(1)若命题p为假命题,命题![]() 为假命题,则命题“
为假命题,则命题“![]() ”为假命题;
”为假命题;
(2)命题“若![]() ,则
,则![]() 或
或![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() 或
或![]() ”;
”;
(3)对立事件一定是互斥事件;
(4)![]() 为两个事件,则P(A∪B)=P(A)+P(B);
为两个事件,则P(A∪B)=P(A)+P(B);
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.

(Ⅰ)求此人到达当日空气质量优良的概率;
(Ⅱ)求此人在该市停留期间只有1天空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com