
| ʩ������x | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| ˮ������y | 330 | 345 | 365 | 405 | 445 | 450 | 455 |
���� ��������������ݵ�ƽ�������õ��������ĵ㣬�������Իع�ֱ�߹��������ĵ㣬��������е�һ��ϵ�����õ����Իع鷽�̣����Ա���Ϊ55���룬Ԥ�������
��� �⣺����֪�ɵã�$\overline{x}$=$\frac{1}{7}$��15+20+25+30+35+40+45��=30��
$\overline{y}$=$\frac{1}{7}$��330+345+365+405+445+450+455����399.3��
�ع鷽��$\widehat{y}$=bx+$\widehat{a}$�е�bΪ4.8��
��$\widehat{a}$=399.3-4.8��30=255.3��
����������Ϊ55kgʱ��ˮ������ԼΪ��$\widehat{y}$=4.8��55+255.3=519.3��
�ʴ�Ϊ��519.3
���� ���⿼�����Իع鷽�̵���Ӧ�ã���һ�������⣬������ؼ����������Իع�ֱ�߱ض������������ĵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -29 | B�� | 29 | C�� | 30 | D�� | -30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
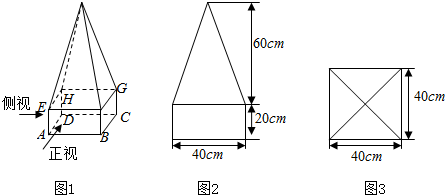
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com