
【题目】设等比数列![]() 的前
的前![]() 项和为
项和为![]() ;数列
;数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)①试确定![]() 的值,使得数列
的值,使得数列![]() 为等差数列;
为等差数列;
②在①结论下,若对每个正整数![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个2,得到一个新数列
个2,得到一个新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试求满足
项和,试求满足![]() 的所有正整数
的所有正整数![]() .
.
科目:高中数学 来源: 题型:
【题目】某种汽车购买时费用为16.9万元,每年应交付保险费、汽油费共0.9万元,汽车的维修保养费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,……依等差数列逐年递增.
(1)求该车使用了3年的总费用(包括购车费用)为多少万元?
(2)设该车使用![]() 年的总费用(包括购车费用)为
年的总费用(包括购车费用)为![]() ),试写出
),试写出![]() 的表达式;
的表达式;
(3)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,
中, ![]() 底面
底面 ![]() ,
, ![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,且
,且 ![]() ,
, ![]() 是
是 ![]() 的中点.
的中点.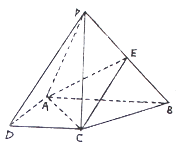
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)若二面角 ![]() 的余弦值为
的余弦值为 ![]() ,求直线
,求直线 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设M=( ![]() ﹣1)(
﹣1)( ![]() ﹣1)(
﹣1)( ![]() ﹣1)满足a+b+c=1(其中a>0,b>0,c>0),则M的取值范围是( )
﹣1)满足a+b+c=1(其中a>0,b>0,c>0),则M的取值范围是( )
A.[0, ![]() )
)
B.[ ![]() ,1)
,1)
C.[1,8)
D.[8,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com