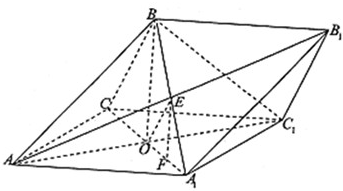
分析:(I)由四边形AA1C1C为平行四边形,知AC=A1C1,由AC=AA1,知△AA1C1为等边三角形,由此能够证明BO⊥平面AA1C1C.
(Ⅱ)连接BA1交AB1于E,过E作EF∥BO交OA1于F,连接OE,由BO⊥平面AA1C1C,AC1?平面AA1C1C,知EF⊥AC1,由OF⊥AC1,OF∩EF=F,EF,OF?平面OA1B,知AC1⊥平面OA1B,由OE?平面OA 1 B,知AC1⊥OE,由此得到∠EOF是二面角的平面角,从而能求出二面角B1-AC1-A1的大小.
解答:解:(I)∵四边形AA
1C
1C为平行四边形,∴AC=A
1C
1,
∵AC=AA
1,∴AA
1=A
1C
1,∴∠AA
1C
1=60°,
∴△AA
1C
1为等边三角形,
同理△ABC
1是等边三角形,
∵O为AC
1的中点,∴BO⊥AC
1,
∵BO?平面ABC
1,平面ABC
1∩平面AA
1C
1C=AC
1,
∴平面ABC
1⊥平面AA
1C
1C,
由面面垂直的性质定理知BO⊥平面AA
1C
1C.
(Ⅱ)连接BA
1交AB
1于E,过E作EF∥BO交OA
1于F,连接OE,
∵BO⊥平面AA
1C
1C,AC
1?平面AA
1C
1C,∴EF⊥AC
1,
又∵OF⊥AC
1,OF∩EF=F,
EF,OF?平面OA
1B,
∴AC
1⊥平面OA
1B,
∵OE?平面OA
1 B,∴AC
1⊥OE,
∴∠EOF是二面角的平面角,
在直角三角形EOF中,OF=
CA1=,
EF=
BO=,
∴∠EOF=
,故二面角B
1-AC
1-A
1的大小为
.
点评:本题考查直线与平面垂直的证明,考查二面角的求法,解题时要认真审题,注意等价转化思想的合理运用.

 在三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面AA1C1C,∠AA1C1=∠BAC1=60°,设AC1与AC相交于点O,如图.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面AA1C1C,∠AA1C1=∠BAC1=60°,设AC1与AC相交于点O,如图.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案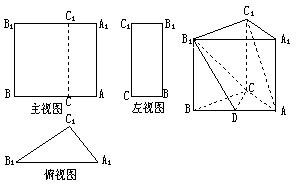 已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,cos∠A1=
已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,cos∠A1=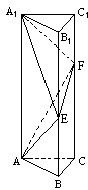 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB=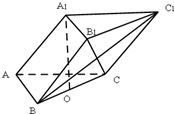 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=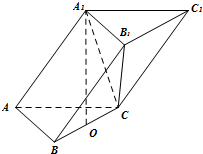 (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=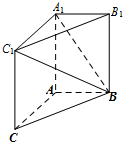 (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.