
【题目】定义:如果函数f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)满足![]()
![]() , ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
, ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
A.(![]() ,
,![]() )
)
B.(![]() ,3)
,3)
C.(![]() , 1)
, 1)
D.(![]() , 1)
, 1)
【答案】C
【解析】解:由题意可知,∵f(x)=x3﹣x2+a,f′(x)=3x2﹣2x
在区间[0,a]存在x1 , x2(a<x1<x2<b),
满足f′(x1)=f′(x2)=![]() =a2﹣a,
=a2﹣a,
∵f(x)=x3﹣x2+a,
∴f′(x)=3x2﹣2x,
∴方程3x2﹣2x=a2﹣a在区间(0,a)有两个不相等的解.
令g(x)=3x2﹣2x﹣a2+a,(0<x<a)
则 ,
,
解得;![]() .
.
∴实数a的取值范围是(![]() , 1)
, 1)
故选:C
【考点精析】认真审题,首先需要了解导数的几何意义(通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 为参数
为参数![]() 和直线
和直线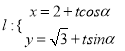
![]() 其中
其中![]() 为参数,
为参数, ![]() 为直线
为直线![]() 的倾斜角
的倾斜角![]() .
.
(1)当![]() 时,求圆上的点到直线
时,求圆上的点到直线![]() 的距离的最小值;
的距离的最小值;
(2)当直线![]() 与圆
与圆![]() 有公共点时,求
有公共点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点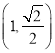 ,离心率为
,离心率为![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 的长轴的两个端点(
的长轴的两个端点(![]() 位于
位于![]() 右侧),
右侧),![]() 是椭圆在
是椭圆在![]() 轴正半轴上的顶点.
轴正半轴上的顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 和
和![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出直线方程;如果不存在,请说明理由.
共线?如果存在,求出直线方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b∈R,ab≠0,给出下面四个命题:①a2+b2≥﹣2ab;② ![]() ≥2;③若a<b,则ac2<bc2;④若
≥2;③若a<b,则ac2<bc2;④若 ![]() .则a>b;其中真命题有( )
.则a>b;其中真命题有( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装销售公司进行关于消费档次的调查,根据每人月均服装消费额将消费档次分为0-500元;500-1000元;1000-1500元;1500-2000元四个档次,针对![]() 两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
| 0~ 500元 | 500~ 1000元 | 1000~ 1500元 | 1500~ 2000元 |
A类 | 20 | 50 | 20 | 10 |
B类 | 50 | 30 | 10 | 10 |
月均服装消费额不超过1000元的人群视为中低消费人群,超过1000元的视为中高收入人群.
(Ⅰ)从![]() 类样本中任选一人,求此人属于中低消费人群的概率;
类样本中任选一人,求此人属于中低消费人群的概率;
(Ⅱ)从![]() 两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(Ⅲ)以各消费档次的区间中点对应的数值为该档次的人均消费额,估计![]() 两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:函数y=log2(x2﹣2x)的单调增区间是[1,+∞),命题q:函数y=![]() 的值域为(0,1),下列命题是真命题的为( )
的值域为(0,1),下列命题是真命题的为( )
A.p∧q
B.p∨q
C.p∧(¬q)
D.¬q
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com