
 在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合:
在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合: ;
; .
. 解:(1)作直线
解:(1)作直线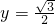 交单位圆于A、B两点,连接OA、OB,
交单位圆于A、B两点,连接OA、OB,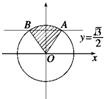
 ≤α≤2kπ+
≤α≤2kπ+ ,k∈z,}.
,k∈z,}. 交单位圆于C、D两点,连接OC、OD,则OC与
交单位圆于C、D两点,连接OC、OD,则OC与 ≤α≤2kπ+
≤α≤2kπ+ ,k∈z,}.
,k∈z,}.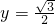 交单位圆于A、B两点,OA与OB围成的区域(阴影部分)即为角α的终边的范围,在[0,2π)内的角的范围为[
交单位圆于A、B两点,OA与OB围成的区域(阴影部分)即为角α的终边的范围,在[0,2π)内的角的范围为[ ,
, ],可得足条件的角α的集合.
],可得足条件的角α的集合. 交单位圆于C、D两点,OC与OD围成的区域(图中阴影部分)即为角α终边的范围,在[0,2π)内的角的范围为[
交单位圆于C、D两点,OC与OD围成的区域(图中阴影部分)即为角α终边的范围,在[0,2π)内的角的范围为[ ,
, ],得足条件的角α的集合.
],得足条件的角α的集合.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com